Rogue wave recreated in laboratory tank

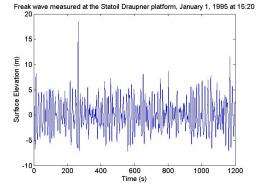
Rogue waves had long been considered a myth by most scientists; little more than tall tales told by sailors, until New Year’s Eve 1985, when a laser affixed to an oil rig captured one off the coast of Norway. Since that time, more of them have been seen by satellite images and scientists have had to scramble to explain the apparent anomalies that seemed to occur without any reasonable explanation.

Into the void stepped Howell Peregrine, using a particular solution to the Schroedinger equation to show that pulse like waves, now called Peregrine solitons, can appear out of sine waves, given the right set circumstances.

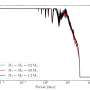
Building on Peregrine’s findings, a team of three researchers; Amin Chabchoub, a mathematician, and two physicists, Norbert Hoffmann Nail Akhmediev, have created what they call a Peregrine rouge wave in a water tank. Using a computer controlled paddle to create very small (1 centimeter) sine waves to simulate normal conditions, and then to create a slight disturbance by precisely changing (modulating) the paddle motion to mimic a sudden slight change in real world weather conditions, they were able to watch as a wave suddenly appeared traveling roughly half as fast as the others and then as it eventually grew to roughly three times their size, which is exactly what was predicted.

Of course, creating a rogue wave in a controlled environment water tub is not nearly enough to explain everything that’s going on out in the open ocean, but it does show that math can be applied in some circumstances to help explain such seemingly random phenomena as giant waves suddenly appearing out of nowhere. The next step for the researchers will of course be creating more realistic environments to see if the model will continue to hold up as more variable are added.

More information: Rogue Wave Observation in a Water Wave Tank, Phys. Rev. Lett. 106, 204502 (2011) DOI:10.1103/PhysRevLett.106.204502

Abstract
The conventional definition of rogue waves in the ocean is that their heights, from crest to trough, are more than about twice the significant wave height, which is the average wave height of the largest one-third of nearby waves. When modeling deep water waves using the nonlinear Schrödinger equation, the most likely candidate satisfying this criterion is the so-called Peregrine solution. It is localized in both space and time, thus describing a unique wave event. Until now, experiments specifically designed for observation of breather states in the evolution of deep water waves have never been made in this double limit. In the present work, we present the first experimental results with observations of the Peregrine soliton in a water wave tank.

© 2010 PhysOrg.com