Number one rules in nature: study

The research, led by Professor Malcolm Sambridge in the Research School of Earth Sciences, shows that events as diverse as the rotation rates of dying stars and the surface areas of rivers all share one thing in common – in nature larger numbers are less likely to occur than smaller ones.

Professor Sambridge said that by applying an obscure mathematical theory called Benford’s law to a range of natural phenomena, he and his colleagues were able to reveal some remarkable relationships across the physical sciences.

“Most physicists would think that the likelihood of a number beginning with a one would occur just as often with numbers beginning with a two or a three or so on,” said Sambridge. “But it turns out this is not the case in the natural world.

“Instead, as Benford’s law shows, roughly 30 per cent of numbers related to real-world events begin with the number one and only 17 per cent begin with a two. And it goes right down to roughly about four per cent beginning with a nine,” he said.

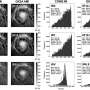
To test the theory the researchers tested 18 data sets containing over 750,000 numbers across a range of natural phenomena, including green-house gas emissions, the masses of giant planets outside our solar system, the number of infectious diseases reported by the World Health Organization, the time it takes a burst from a gamma ray to reach your eye and the periods between the flipping of the earth’s magnetic poles.

“Much to our surprise we found that Benford’s law largely holds true in all these areas,” said Professor Sambridge. “The natural world is littered with a surplus of the digit one.”

The study also led to the detection of a physical event for the first time ever – identifying a previously overlooked earthquake which took place in Canberra during the 2004 Asian tsunami.

“One of the things we are interested in is automated methods of detecting an earthquake,” said Sambridge. “We found that Benford’s law can be used for exactly that purpose.

“By taking the first digits of the counts of a seismometer, which measures motions in the ground caused by earthquakes, we can quite clearly see the onset of an earthquake.

“This also means that we can use computers to detect when waves from an earthquake arrive at a recording station in an entirely new way,” he said.

Provided by Australian National University