September 27, 2010 feature
Scientists develop new way to decipher hidden messages in symbols
(PhysOrg.com) -- Almost all information, in a sense, can be represented by symbols. In order to extract this embedded information, the symbols and the rules governing their sequence formation need to be deciphered. There are many examples of information residing in symbols, although the most familiar is probably written language. In addition to the sequences of letters that make up words, and sequences of words that make up sentences, there are lexical and grammatical rules that govern how letters and words can be combined, respectively, so that not all sequences of letters and words are possible. In a recent study, a group of scientists from Italy has developed a generic method to extract information from any type of symbolic sequential data, even when a "dictionary" of symbol sequences is not known beforehand.
The researchers, Roberta Sinatra, Daniele Condorelli, and Vito Latora, from the University of Catania and the Scuola Superiore di Catania, are publishing their study in an upcoming issue of Physical Review Letters. As they explained, a few of the many examples where information has to be extracted from sequences of symbols are protein sequences, DNA nucleotides, musical notation, dance movements, texts written in an unknown language, and others. Having a general method to extract the information in any type of symbol sequence could be extremely useful for deciphering encoded data.
"I think that it is interesting that one can construct a lexicon for every non-random collection of symbolic data, just by means of statistical methods," Sinatra told PhysOrg.com. "In fact, if a sequence of symbols encodes some information, it cannot be random and probably is made up of fundamental units that perform the same role that words do in language. Therefore, by extracting these significant units, it is possible to construct a dictionary also for proteins, dances, and music, since they can all be represented in terms of sequences of symbols that show non-trivial statistical properties."
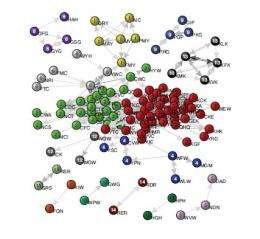
In their method, the researchers first converted the symbol sequences into a network based on a dictionary of significant strings of symbols extracted from the sequences. They called these significant strings “motifs,” which are the equivalent of words in a language, since they deviate from randomness. The motifs represent the fundamental “bricks” that sequences are made of by following rules of combination syntax. When converted to a network, these motifs form the nodes of the network. The links between the nodes represent a significant occurrence of two motifs in the same sequence (the equivalent of a phrase or sentence). So a weighted, directed link between two nodes means that the nodes often appear together in a sequence in a certain order. For example, if “the” and “end” were two nodes, there would likely be a directed link between them to represent the existence of the common phrase “the end.”
“We know that if we type at random on a keyboard, it is unlikely that we end up forming a sentence or even a word that makes sense,” Sinatra explained. “Similarly, we know that if we select some letters, say E,H,M,O, we know that we need to put them in a specific order, for example HOME and not HMOE, to encode some information in it. By looking at how many times the sequence HOME and the sequence HMOE appear in a text, we can understand which string contains a message and which is just there by chance (due to a typo, for example). However, we know that important information is contained not only at the level of words, but also in sentences and in general in how words are coexpressed. So it is unlikely that we find the words "the" and "for" next to each other or a verb followed by another verb ("I sit go"). This is why we introduce the concept of the network of motifs: it embeds the information of how words correlate in sequences of symbols.”
By analyzing the network of motifs, the researchers could identify significant patterns, and then extract important information encoded in the original data simply from the way the network is structured. In particular, information about the network's community structures, i.e., the groups of nodes that are tightly connected among themselves and weakly connected to the rest of the network, proved helpful for extracting encoded messages. The researchers demonstrated the approach for three different data sets: the human proteome (the protein equivalent of the genome), Twitter posts, and dynamical systems. For instance, in the proteome example, the communities of the motif network can identify those parts of proteins (sequences of amino acids) called functional domains that specify the protein function. In these systems and others, the motif network approach can be very useful for processing information from extremely large amounts of symbolic data.
“With this method, we are able to compact information deriving from an entire ensemble of sequences, like all the proteins of a species or all the tweets posted in one day in Twitter, in just one object: the network of motifs,” Sinatra said. “Of course, one could study in great detail only one sequence, for example one protein or one post, and have complete knowledge of what information that protein or post means. But this would be equivalent to reading just one sentence of an entire book: what can one understand from just one sentence if a book is made up of thousands of them? This is why we usually read the summary on the back cover of a book. Well, the network of motifs plays exactly this role: it 'summarizes' the entire ensemble of sequences, providing information on what the main message is.”
More information: Roberta Sinatra, Daniele Condorelli, and Vito Latora. “Networks of motifs from sequences of symbols.” To be published. Available at arXiv:1002.0668v2. arxiv4.library.cornell.edu/abs/1002.0668v2
Copyright 2010 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.