November 9, 2007 feature
Nonlocality of a Single Particle Demonstrated Without Objections
Usually when physicists talk about nonlocality in quantum mechanics, they’re referring to the fact that two particles can have immediate effects on each other, even when separated by large distances. Einstein famously called the phenomena “spooky interaction at a distance” because information about a particle seems to be traveling faster than the speed of light, violating the laws of causality.
Although the idea is counterintuitive, nonlocality is now widely accepted by physicists, albeit almost exclusively for two-particle systems. So far, no experiment has sufficiently demonstrated the nonlocality of a single particle, although explanations have been proposed since 1991 (starting with Tan, Walls, and Collett).
Since then, the issue has been strongly debated by physicists. In 1994, Lucien Hardy proposed a modified scheme of Tan, Walls, and Collett’s claim. However, others (notably Greenberger, Horne, and Zeilinger) objected to Hardy’s scheme, claiming that it was really a multi-particle effect in disguise, and could not be demonstrated experimentally.
Now, Jacob Dunningham from the University of Leeds and Vlatko Vedral from the University of Leeds and the National University of Singapore have modified Hardy’s scheme, publishing their results in a recent issue of Physical Review Letters. By eliminating all unphysical inputs, their scheme allows for a real experiment, and ensures that only a single particle exhibits nonlocality. Plus, Dunningham and Vedral’s scheme not only applies to single photons, but to atoms and single massive particles, as well.
“The greatest significance of this work is that it shows how superposition and entanglement are the same ‘mystery,’” Dunningham explained to PhysOrg.com. “Feynman famously said that superposition is the only mystery in quantum mechanics, but more recently entanglement has been widely considered as an additional fundamental feature of quantum physics. Here we show that they are one and the same.”
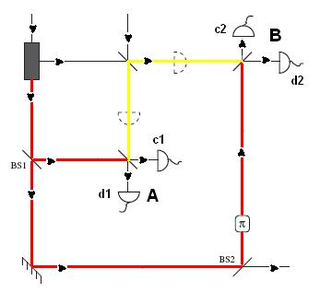
In Hardy’s original scheme, one photon and a vacuum state arrive at a beam splitter, a glass prism that splits a beam of light in two. Two observers, Alice and Bob, have the option to either measure one of the beams, or to combine their beam with a coherent light beam, split the resulting beam with another beam splitter, and then measure the two outputs (also known as a “homodyne detection”).
Alice and Bob’s decisions could result in four possible combinations. First, if they both measure their beam from the original beam splitter, only one will detect a photon. Second, if Alice adds a coherent state to her beam while Bob measures his original split beam, Alice has two chances of detecting a photon, at the two outputs (c1, d1) of her beam splitter. Hardy showed that, if Alice detected a photon at c1, Bob would not detect a photon; but if Alice detected a photon at d1, Bob must detect a photon. In the third possibility, the roles of Alice and Bob are simply switched, with the same results.
In the fourth possibility, both Alice and Bob make homodyne detections. If they both detect particles at their d detectors (d1 and d2, respectively), then they both infer that the other must detect a photon from the original source. This is a problem, because they cannot both be right—there is only one original photon.
Hardy argued that this scheme demonstrates the nonlocality of a single particle when one eliminates the implicit local assumption that Alice’s result is independent of Bob’s measurement (and vice versa). Rather, one observer’s result does depend on the other’s measurement, so that, due to a nonlocal influence, the second observer’s measurement is determined by the first observer’s measurement.
“If we try and interpret this experimental scheme using only classical physics, it turns out that it is not possible for the outcomes of all four of the proposed experiments to be consistent,” Vedral explained. “The outcome of experiment four is not consistent with the others. Classical physics assumes that the particle exists independent of our observing (or measuring) it, and also that one measurement cannot influence a particle at a distance.
“For example, what Alice does cannot affect Bob’s particle,” he continued. “Since the outcomes of this scheme are not consistent with classical physics, we must drop one of the assumptions. This means that if we wish to maintain the view that reality exists independent of our measurements (e.g. the moon is there even if we don’t look at it), we are forced to accept that the world is nonlocal. This is how Hardy based his argument for nonlocality on the contradictory outcomes.”
However, Greenberger, Horne, and Zeilinger took issue with Hardy’s argument, pointing out that combining a photon and a vacuum does not result in an observable state, and therefore could not be performed in a real experiment. They even attempted a scheme that didn’t use these so-called “partlycle” superpositions, but found that the entire system then demonstrated nonlocality, making it impossible to attribute nonlocality to a single particle.
Dunningham and Vedral’s proposal makes a few key changes to Hardy’s scheme. First, instead of using coherent states of a photon and vacuum, they use mixed states—a mixture of coherent states averaged over all phases of the particles. In this way, they don’t violate superselection rules and so avoid objections that have been raised before.
Then, for the homodyne detections, they ensure that the coherent light beam combining with the original beam has the same phase. Having the same phase is key, as it ensures that Alice and Bob can consistently compare their measurement results. The coherent states are only classically correlated with the single particle state. This means that, when Alice and Bob perform their homodyne detections, and one detection influences the other, the nonlocality must stem from the original single-particle state.
Because the main importance is maintaining a common average phase—but not a specific phase—Dunningham and Vedral’s scheme could, in principle, be carried out in the laboratory. Also, the researchers suggest that, by using beam splitters for atoms and atom detectors, their scheme could conceivably verify the nonlocality of a single massive particle, in addition to a massless photon.
“An important feature of this work is that it shows how this experiment could be carried out without violating the number conservation superselection rule,” Dunningham said. “This is important because people are often happy to accept such violations for massless particles (e.g. photons) but not for massive particles such as atoms. By avoiding this violation altogether, we show that the outcomes of this proposed experiment should be the same for both massive and massless particles.”
The scientists note an interesting comparison of their result to a principle of Leibniz’s metaphysics, the identity of indiscernibles. According to the principle, a pair of entangled quantum particles must be indiscernible from a single particle, since both objects have in common all the same properties—this is the only stipulation of the principle, number being irrelevant. The single-state nonlocality demonstrated here reinforces the equivalence of a single state and an entangled state—giving more credence to the position that quantum field theory, where fields are fundamental and particles secondary, is a close representation of reality.
More information: Dunningham, Jacob and Vedral, Vlatko. “Nonlocality of a Single Particle.” Physical Review Letters 99, 180404 (2007).
Copyright 2007 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.