Numbers follow a surprising law of digits, and scientists can't explain why

Does your house address start with a 1? According to a strange mathematical law, about 1/3 of house numbers have 1 as their first digit. The same holds true for many other areas that have almost nothing in common: the Dow Jones index history, size of files stored on a PC, the length of the world’s rivers, the numbers in newspapers’ front page headlines, and many more.

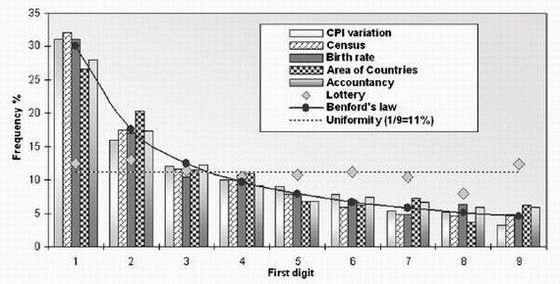
The law is called Benford’s law after its (second) founder, Frank Benford, who discovered it in 1935 as a physicist at General Electric. The law tells how often each number (from 1 to 9) appears as the first significant digit in a very diverse range of data sets.

Besides the number 1 consistently appearing about 1/3 of the time, number 2 appears with a frequency of 17.6%, number 3 at 12.5%, on down to number 9 at 4.6%. In mathematical terms, this logarithmic law is written as F(d) = log[1 + (1/d)], where F is the frequency and d is the digit in question.

If this sounds kind of strange, scientists Jesús Torres, Sonsoles Fernández, Antonio Gamero, and Antonio Sola from the Universidad de Cordoba also call the feature surprising. The scientists published a letter in the European Journal of Physics called “How do numbers begin? (The first digit law),” which gives a short historical review of the law. Their paper also includes useful applications and explains that no one has been able to provide an underlying reason for the consistent frequencies.

“The Benford law has been an intriguing question for me for years, ever since I read about it,” Torres, who specializes in plasma physics, told PhysOrg.com. “I have used it as a surprising example at statistical physics classes to arouse the curiosity of my pupils.”

Torres et al. explain that, before Benford, a highly esteemed astronomer named Simon Newcomb discovered the law in 1881, although Newcomb’s contemporaries did not pay much attention to his publication. Both Benford and Newcomb stumbled upon the law in the same way: while flipping through pages of a book of logarithmic tables, they noticed that the pages in the beginning of the book were dirtier than the pages at the end. This meant that their colleagues who shared the library preferred quantities beginning with the number one in their various disciplines.

Benford took this observation a step further than Newcomb, and began investigating other groups of numbers, finding that the “first digit law” emerged in groups as disparate as populations, death rates, physical and chemical constants, baseball statistics, the half-lives of radioactive isotopes, answers in a physics book, prime numbers, and Fibonacci numbers. In other words, just about any group of data obtained by using measurements satisfies the law.

On the other hand, data sets that are arbitrary and contain restrictions usually don’t follow Benford’s law. For example, lottery numbers, telephone numbers, gas prices, dates, and the weights or heights of a group of people are either random or arbitrarily assigned, and not obtained by measurement.

As Torres and his colleagues explain, scientists in the decades following Benford performed numerous studies, but discovered little more about the law other than racking up a wide variety of examples. However, scientists did discover a few curiosities. For one, when investigating second significant digits of data sets, the law still held, but with less importance. Similarly, for the third and fourth digits, the appearance of the numbers started becoming equal, leveling out at a uniform 10% for the fifth digit. A second discovery attracted even more scientific interest:

“In 1961, Pinkham discovered the first general relevant result, demonstrating that Benford’s law is scale invariant and is also the only law referring to digits which can have this scale invariance,” the scientists wrote in their letter. “That is to say, as the length of the rivers of the world in kilometers fulfill Benford’s law, it is certain that these same data expressed in miles, light years, microns or in any other length units will also fulfill it.”

Torres et al. also explain that in the last years of the 20^th century, some important theoretical advances have been proven (base invariance, unicity, etc.), mainly by Ted Hill and other mathematicians. While some cases can be explained (for example, house addresses almost always start with 1’s, and lower numbers must occur before higher numbers), there is still no general justification for all examples. The scientists also explain that there is no a priori criteria that tells when a data set should or should not obey the law.

“Nowadays there are many theoretical results about the law, but some points remain in darkness,” said Torres. “Why do some numerical sets, like universal physical constants, follow the law so well? We need to know not only mathematical reasons for the law, but also characterize this set of experimental data. For example, what are their points of contact? Where they come from? Apparently, they are independent.

”I hope the general necessary and sufficient conditions will be discovered in the future—many people are interested in the law, especially economists—but I also know it could be not possible ever,” he added, mentioning Godel.

Nevertheless, scientists have been using the law for many practical applications. For example, because a year’s accounting data of a company should fulfill the law, economists can detect falsified data, which is very hard to manipulate to follow the law. (Interestingly, scientists found that numbers 5 and 6, rather than 1, are the most prevalent, suggesting that forgers try to “hide” data in the middle.)

Benford’s law has also been recently applied to electoral fraud in order to detect voting anomalies. Scientists found that the 2004 US presidential election showed anomalies in the state of Florida, as well as fraud in Venezuela in 2004 and Mexico in 2006.

“The story about how it was discovered—twice—from dirty pages … it is almost incredible,” said Torres. “Benford's law has undeniable applications, and this useful aspect was not clear when the law was discovered. It seemed to be only a math curiosity. For me, this is an example of how simplicity can be unexpectedly marvelous.”

For more details on Benford’s law, the highly readable letter is temporarily available at:
www.iop.org/EJ/abstract/0143-0807/28/3/N04 (with free registration).

Citation: Torres, J. Fernández, S., Gamero, A., Solar, A. “How do numbers begin? (The first digit law).” Eur. J. Phys. 28 (2007) L17-25.

Copyright 2007 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.