April 6, 2007 feature
World's economies show similarities in economic inequality
Economists who yearn for the redistribution of wealth in an ideal society are up against history. According to a recent study, the uneven distribution of wealth in a society appears to be a universal law that holds true for economies in many different societies, from ancient Egypt to modern Japan and the U.S. This distribution may reflect a simple natural law analogous to a 100-year-old theory describing the distribution of energy in a gas.
Scientists Arnab Chatterjee and Bikas Chakrabarti from the Saha Institute of Nuclear Physics, along with Sitabhra Sinha of the Institute of Mathematical Sciences, both in India, have analyzed a variety models explaining different sets of data, and found striking similarities. The results show that the poorer majority of the population follows one distribution, while a small proportion of the wealthiest people veers off in a tail following a power-law distribution, in essence reflecting how “the rich get richer.”
The studies included large sets of data from sources such as income tax returns and net values of assets in societies including Japan, the U.S., the UK, India, and nineteenth century Europe. The data, taken from a large number of recent publications by several groups, represented a variety of different economies and stages of development. Generally, the lower 90% of the population (in terms of income) followed a log-normal distribution, characterized by an initial rapid rise in population followed by a rapid fall as income increased.
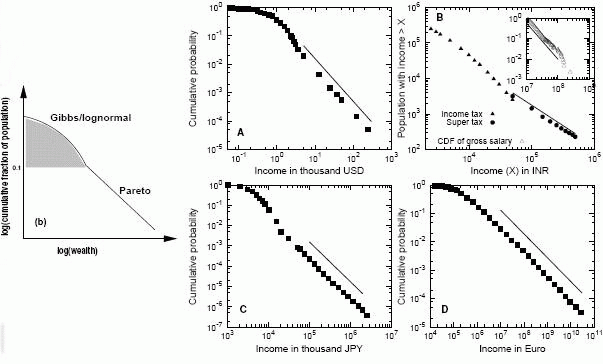
However, the top 2-10% of the population deviated from this bulk distribution, as scientists discovered more very rich people than would be expected using the log-normal model. Instead, this top tier followed a power law with a certain exponent called the Pareto exponent, named after Vilfredo Pareto, who first observed this power law in the 1890s.
“While the distribution of the richest 10% does indeed follow a different behavior (power law) than the rest (Gibbs or log-normal), one need not assume different dynamics at work in the two cases,” Chatterjee explained to PhysOrg.com. “In fact, both types of distributions can arise from the same model. In the case of the random savings model, the agents having the highest savings fractions will have a higher probability of ending up in the richest 10% of the population, while in the random thrift model, the agents with higher thrift value generally tend to be the richest.
“As an agent gets richer, a feedback effect occurs by which the rich are more likely to gain from a transaction than the poorer agents—thereby resulting in an accumulation of assets for the richer players that is manifested as a power law tail.”
When comparing these income and wealth distributions to a physical model called the Gibbs distribution, the scientists found that the economic model of the poorer 90% seemed to fit very well with this natural law. Proposed in the late 1800s, the Gibbs distribution is a thermodynamic model that describes the distribution of energy in an ideal gas in equilibrium.
The economic model and the gas model share basic characteristics. As Chatterjee et al. explain, the asset- (e.g. money-) trading process can be viewed as a molecule scattering process—in both cases, assets or molecules are conserved (on the time scale of the model). Also, even though an individual does not see asset exchanges as random, the scientists show that, from a global level, exchanging assets or scattering molecules are indeed random processes.
“As described in our paper, the Gibbs form seems to be a better fit for the data than the log-normal form (which is preferred by many economists),” Chatterjee explained. “Note, for a particular [savings factor], the resultant [distribution] only fits the lower 90% of the population. To fit the entire range, including the power law tail, one needs a suitably distributed saving propensity. In the thrift model, one obtains realistic values of the Pareto exponent (i.e., as seen in society) by assuming a distribution of the thrift parameter. Hence, both these models can explain both the features of the observed income distribution.”
Aside from these general models, the scientists also discovered some interesting details within their results. When comparing wealth (i.e. one’s net worth) with income, they found that wealth is much more unequally distributed than income (wealth models always have lower Pareto exponents, for any society). Also, while most of the data for the models is based on individuals, data from companies also seemed to follow the same models.
Even though the model shows a widespread inequality among citizens in a society, however, the scientists’ findings might also provide guidance for experts trying to distribute wealth more evenly.
“With uniform savings and large saving propensity, our model would yield a narrow peaked income distribution, which corresponds to a socialist economy,” Chatterjee said. “Note that, here, the super-rich are absent, and the bulk of the population is described by a narrow most-probable income distribution, or everybody ending up with the average money in the market—a socialist’s ideal dream.”
Since the richer agents demonstrate certain characteristics in savings and thrift, the scientists explain that certain characteristics might make citizens in a society “more” financially equal.
“A way to exercise this would be to modify the saving patterns of the individuals, making all of them have a similar and large saving propensity, to be precise. In isolated sectors where such manipulations with savings propensities were possible, our predicted effects had indeed been seen earlier by social statisticians (such as J. Angle) and analysts (such as G. Willis and J. Mimkes).
“In the thrift model,” Chatterjee continued, “introducing different distributions of thrift among the agents can result in more or less equitable distributions. Also, introducing certain forms of taxation in random asset exchange models have resulted in more equitable distributions. These could help experts make policies for a more equitable distribution of wealth in society.”
Citation: Chatterjee, Arnab, Sinha, Sitabhra, and Chakrabarti, Bikas K. “Economic Inequality: Is it Natural?” Currently at arxiv.org/abs/physics/0703201 ; To be published in Current Science.
Copyright 2007 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.





















