May 8, 2009 feature
New Pattern Found in Prime Numbers

(PhysOrg.com) -- Prime numbers have intrigued curious thinkers for centuries. On one hand, prime numbers seem to be randomly distributed among the natural numbers with no other law than that of chance. But on the other hand, the global distribution of primes reveals a remarkably smooth regularity. This combination of randomness and regularity has motivated researchers to search for patterns in the distribution of primes that may eventually shed light on their ultimate nature.
In a recent study, Bartolo Luque and Lucas Lacasa of the Universidad Politécnica de Madrid in Spain have discovered a new pattern in primes that has surprisingly gone unnoticed until now. They found that the distribution of the leading digit in the prime number sequence can be described by a generalization of Benford’s law. In addition, this same pattern also appears in another number sequence, that of the leading digits of nontrivial Riemann zeta zeros, which is known to be related to the distribution of primes. Besides providing insight into the nature of primes, the finding could also have applications in areas such as fraud detection and stock market analysis.
“Mathematicians have studied prime numbers for centuries,” Lacasa told PhysOrg.com. “New insights and concepts coming from nonlinear science, such as multiplicative processes, help us to look at prime numbers from a different perspective. According to this focus, it becomes significant that even today it is still possible to discover unnoticed hints of statistical regularity in such sequences, without being an expert in number theory. However, the most significant issue in this work is not to unveil this pattern in primes and Riemann zeros, but to understand the reason and implications of such unexpected structure, not just for number theoretical issues but, interestingly, for other disciplines as well. For instance, these results deepen our understanding of correlations in systems composed of many elements.”
Benford’s law (BL), named after physicist Frank Benford in 1938, describes the distribution of the leading digits of the numbers in a wide variety of data sets and mathematical sequences. Somewhat unexpectedly, the leading digits aren’t randomly or uniformly distributed, but instead their distribution is logarithmic. That is, 1 as a first digit appears about 30% of the time, and the following digits appear with lower and lower frequency, with 9 appearing the least often. Benford’s law has been shown to describe disparate data sets, from physical constants to the length of the world’s rivers.
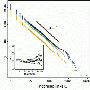
Since the late ‘70s, researchers have known that prime numbers themselves, when taken in very large data sets, are not distributed according to Benford’s law. Instead, the first digit distribution of primes seems to be approximately uniform. However, as Luque and Lacasa point out, smaller data sets (intervals) of primes exhibit a clear bias in first digit distribution. The researchers noticed another pattern: the larger the data set of primes they analyzed, the more closely the first digit distribution approached uniformity. In light of this, the researchers wondered if there existed any pattern underlying the trend toward uniformity as the prime interval increases to infinity.
The set of all primes - like the set of all integers - is infinite. From a statistical point of view, one difficulty in this kind of analysis is deciding how to choose at “random” in an infinite data set. So a finite interval must be chosen, even if it is not possible to do so completely randomly in a way that satisfies the laws of probability. To overcome this point, the researchers decided to chose several intervals of the shape [1, 10d]; for example, 1-100,000 for d = 5, etc. In these sets, all first digits are equally probable a priori. So if a pattern emerges in the first digit of primes in a set, it would reveal something about first digit distribution of primes, if only within that set.
By looking at multiple sets as d increases, Luque and Lacasa could investigate how the first digit distribution of primes changes as the data set increases. They found that primes follow a size-dependent Generalized Benford’s law (GBL). A GBL describes the first digit distribution of numbers in series that are generated by power law distributions, such as [1, 10d]. As d increases, the first digit distribution of primes becomes more uniform, following a trend described by GBL. As Lacasa explained, both BL and GBL apply to many processes in nature.
“Imagine that you have $1,000 in your bank account, with an interest rate of 1% per month,” Lacasa said. “The first month, your money will become $1,000*1.01 = $1,010. The next month, $1,010*1.01, and so on. After n months, you will have $1,000*(1.01)^n. Notice that you will need many months to go from $1,000 to $2,000, while to go from $8,000 to $9,000 will be much easier. When you analyze your accounting data, you will realize that the first digit 1 is more represented than 8 or 9, precisely as Benford's law dictates. This is a very basic example of a multiplicative process where 0.01 is the multiplicative constant.
“Physicists have shown that many processes in nature can be modeled as stochastic multiplicative processes, where the previously constant value of 0.01 is now a random variable and the data equivalent to the money of our latter example is another random variable with an underlying distribution 1/x. Stochastic processes with such distributions are shown to follow BL. Now, many other phenomena fit better to a stochastic process with a more general underlying probability x^[-alpha], where alpha is different from one. The first digit distribution related with this general power law distribution is the so-called Generalized Benford law (which converges to BL for alpha = 1).”
Significantly, Luque and Lacasa showed in their study that GBL can be explained by the prime number theorem; specifically, the shape of the mean local density of the sequences is responsible for the pattern. The researchers also developed a mathematical framework that provides conditions for any distribution to conform to a GBL. The conditions build on previous research, which has shown that Benford behavior could occur when a distribution follows BL for particular values of its parameters, as in the case of primes. Luque and Lacasa also investigated the sequence of nontrivial Riemann zeta zeros, which are related to the distribution of primes, and whose distribution of the zeros is considered to be one of the most important unsolved mathematical problems. Although the distribution of the zeros does not follow BL, here the researchers found that it does follow a size-dependent GBL, as in the case of the primes.
The researchers suggest that this work could have several applications, such as identifying other sequences that aren’t Benford distributed, but may be GBL. In addition, many applications that have been developed for Benford’s law could eventually be generalized to the wider context of the Generalized Benford’s law. One such application is fraud detection: while naturally generated data obey Benford’s law, randomly guessed (fraudulent) data do not, in general.
“BL is a specific case of GBL,” Lacasa explained. “Many processes in nature can be fitted to a GBL with alpha = 1, i.e. a BL. The hidden structure that Benford's law quantifies is lost when numbers are artificially modified: this is a principle for fraud detection in accounting, where the combinatorial mechanisms associated to accounting sets are such that BL applies. The same principle holds for processes following GBL with a generic alpha, where BL fails. Last, for processes whose underlying density is not x^(-alpha) but 1/logN, a size-dependent GBL would be the correct hallmark.”
More information: Bartolo Luque and Lucas Lacasa. “The first digit frequencies of primes and Riemann zeta zeros.” Proceedings of the Royal Society A. doi: 10.1098/rspa.2009.0126.
• Join PhysOrg.com on Facebook!
• Follow PhysOrg.com on Twitter!
Copyright 2009 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.