A new kind of counting: Scientists develop computer algorithm to solve previously unsolvable counting problems
(PhysOrg.com) -- How many different sudokus are there? How many different ways are there to color in the countries on a map? And how do atoms behave in a solid? Researchers at the Max Planck Institute for Dynamics and Self-Organization in Göttingen and at Cornell University (Ithaca, USA) have now developed a new method that quickly provides an answer to these questions.
In principle, there has always been a way to solve them. However, computers were unable to find the solution as the calculations took too long. With the new method, the scientists look at separate sections of the problem and work through them one at a time. Up to now, each stage of the calculation has involved the whole map or the whole sudoku. The answers to many problems in physics, mathematics and computer science can be provided in this way for the first time. (New Journal of Physics, February 4, 2009)
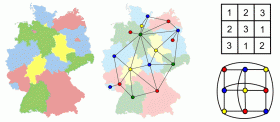
Whether sudoku, a map of Germany or solid bodies - in all of these cases, it’s all about counting possibilities. In the sudoku, it is the permitted solutions; in the solid body, it is the possible arrangements of atoms. In the map, the question is how many ways the map can be colored so that adjacent countries are always shown in a different color. Scientists depict these counting problems as a network of lines and nodes. Consequently, they need to answer just one question: How many different ways are there to color in the nodes with a certain number of colors? The only condition: nodes joined by a line may not have the same color. Depending on the application, the color of a node is given a completely new significance. In the case of the map, "color" actually means color; with sudoku the "colors" represent different figures.
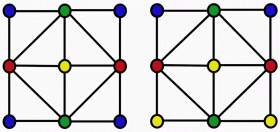
"The existing algorithm copies the whole network for each stage of the calculation and only changes one aspect of it each time," explains Frank van Bussel of the Max Planck Institute for Dynamics and Self-Organization (MPIDS). Increasing the number of nodes dramatically increases the calculation time. For a square lattice the size of a chess board, this is estimated to be many billions of years. The new algorithm developed by the Göttingen-based scientists is significantly faster. "Our calculation for the chess board lattice only takes seven seconds," explains Denny Fliegner from MPIDS.
This is how it’s done: With the new method, the researchers move through the network node by node. As if the computer program were short-sighted, it only ever looks at the next node point and not at the whole network. At the first node point, it cannot finalize the color selection as it would have to know how all the other nodes are connected to each other. However, instead of answering this question, the program notes down a formula for the first lattice point which contains this uncertainty as an unknown quantity. As it progresses through the network, all the connections become visible and the unknown quantities are eliminated. Having arrived at the final node point, the program’s knowledge of the network is complete.
This new method can be used on much more complicated cases than the existing standard algorithm. "We can now answer many questions in physics, graph theory and computer science that have hitherto been practically unsolvable," says Marc Timme from MPIDS. "For example, our method can be applied to antiferromagnetic solids," he adds. In these solid bodies, every atom has an internal rotational pulse, called spin, which can have different values. Usually, adjacent atoms exhibit different spins. It is now possible to calculate the number of possible spin arrangements, which will allow physicists to draw conclusions about the fundamental characteristics of the thermodynamics of solid bodies.
More information: Marc Timme, Frank van Bussel, Denny Fliegner, and Sebastian Stolzenberg, Counting Complex Disordered States by Effiecient Pattern Matching: Chromatic Polynomials and Potts Partition Functions, New Journal of Physics 11 (2009), 023001, February 4th, 2009, www.iop.org/EJ/abstract/1367-2630/11/2/023001/
Provided by Max-Planck-Institute