June 7, 2013 report
Bayesian statistics theorem holds its own - but use with caution
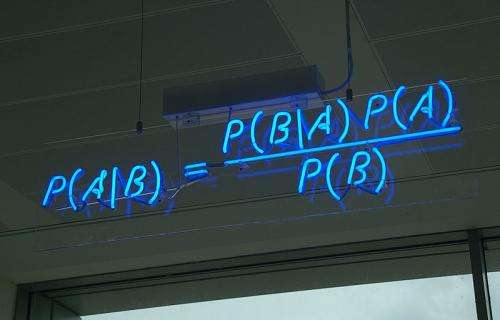
(Phys.org) —In a Perspective in Science magazine this week, a Stanford Professor of Statistics re-examines Bayes' Theorem, its varying fortunes over the two-and-a-half centuries since it was proposed, and its current boom in popularity and likely future.
Bayes' Theorem was proposed by Thomas Bayes in the 18th century, and it combines newly acquired data with prior data to predict an outcome. In his paper, Professor Bradley Efron of Stanford University, presents the example of predicting whether twins are likely to be fraternal or identical in his overview of the theorem.
In Professor Brad Efron's example, there are two categories of data to be considered: the newly acquired data (that sonograms show a pregnant woman is carrying twin boys), and the prior data (the fact that one-third of twins are identical). Identical twins are twice as likely to produce twin boy sonograms because identical twins are always the same sex while fraternal twins have only a 50:50 chance of being the same sex.
Bayes' theorem combines these data in the formula.
P(A|B) = [P(B|A) x P(A)] / P(B)
where P(A|B) is the conditional probability of A given B, and P(B|A) is the conditional probability of B given A. In the example, A is the twins being identical, a prior with probability = 1/3. B is the "sonogram shows twin boys". Genetics imply P(B|A) = 1/2, giving P(A|B) = (1/2) x (1/3) / (1/3) = 1/2.
The formula correctly predicts the twins have an equal probability of being fraternal or identical.
The theorem has proved its worth, such as in 2012 when it was used to successfully predict the outcome of the U.S. presidential election in all 50 states before the final vote counts were available. Despite its success it has always been regarded with some suspicion by statisticians, particularly because it has been used when genuine prior data is unavailable or uncertain.
Efron also compares more recent statistical theories such as frequentism to Bayes' theorem, and looks at the newly proposed fusion of Bayes' and frequentist ideas in Empirical Bayes. Frequentism has dominated for a century and does not use prior information, considering future behavior instead.
Statistical theorems are important because they are widely used in areas such as medical research. Efron reports that in his work as an editor of a statistics journal, he found around 25 percent of papers used Bayers' theorem and most were based on uninformative priors, which counts against it, but on the other hand he notes that the current environment of data being produced in "fire hose" quantities means Bayers' theorem could effectively connect disparate inferences.
Efron uses another example to explain the problem: a study of 52 men with prostate cancer and 50 healthy controls looked at the activity of 6033 genes in the hope of identifying genes expressed differently in the patients. They calculated a test statistic (z) for each gene, with a normal bell-shaped distribution if there was no difference between patients and controls, but with larger values if there were differences.
The resulting histogram looked normal except for 28 of the genes on the right of the distribution, having z>3.40 values. These could represent real or false discoveries, since some z values are bound to be large even in the null hypothesis (no difference between patient/control gene expression). The frequentist theorem predicts false discovery rate (FDR) to be below 10%, which means only 2.8 of these are false. The Bayes theorem suggests the probability of nullness is also 10%, but no prior evidence is used, and the prior is estimated from the data itself. Efron says this "statistical jujitsu" is Empirical Bayes, which is essentially a fusion of frequentist and Bayes ideas that says that when there are large numbers of parallels (as in the 6033 gene study), the data "carry within them their own prior distribution."
Efron warns that Bayes' theorem can be used if genuine prior information is available but caution is needed if there are uninformative priors. For parallel cases, Empirical Bayes methods can be used effectively.
More information: Bayes' Theorem in the 21st Century, Science 7 June 2013: Vol. 340 no. 6137 pp. 1177-1178 DOI: 10.1126/science.1236536
Abstract
The term "controversial theorem" sounds like an oxymoron, but Bayes' theorem has played this part for two-and-a-half centuries. Twice it has soared to scientific celebrity, twice it has crashed, and it is currently enjoying another boom. The theorem itself is a landmark of logical reasoning and the first serious triumph of statistical inference, yet is still treated with suspicion by most statisticians. There are reasons to believe in the staying power of its current popularity, but also some signs of trouble ahead.
Journal information: Science
© 2013 Phys.org