A solution that counts: Long-standing mathematical conjecture finally proved

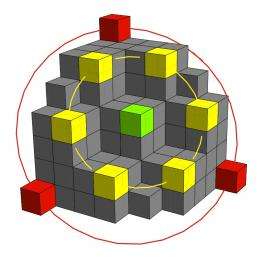
Even mathematicians play with building blocks. At least if they are interested in so-called plane partitions, which are visualized with columns of "building blocks" (cubes) on a surface resembling a chessboard. When "building" such plane partitions, the mathematicians must adhere to certain rules: No column may be higher than the width of the surface, or than another column behind it or left of it. The question of how many column permutations may be built on a given surface area is easily answered, thanks to a specific formula. However, it becomes trickier if the permutations must follow stipulated symmetries, or if, instead of counting the permutations, you wish to count its constituents. Although formulas have been designed to do this too, the crux of the matter is that not all of these formulas have really been proved to be accurate. It is only conjectured.

The Proof Is In The Computer

The proof that one of these formulas is correct has now been found by Dr. Christoph Koutschan and Dr. Manuel Kauers from the Research Institute for Symbolic Computation of the Johannes Kepler University Linz, Austria, in cooperation with Prof. Doron Zeilberger from the United States. It is a formula that is employed for calculating the individual components in totally symmetric plane partitions. Dr. Koutschan comments on the special method they used to find the proof: "We let the computer do the work! In some areas of mathematics this has long been a matter of routine." The underlying principle of such computer-assisted proof is simple. In order to prove A=B, the computer calculates an adjoint equation U=V with the following two properties: "If U=V is true, then A=B is also true" and "it is easy to verify that U=V".

Although it may sound easy, it represents a great challenge, according to Dr. Koutschan: "This method does not work for every equation. The most important step was for us to convert the Andrews-Robbins conjecture into a suitable form for the computer to be able to prove it." The fact that the adjoint equation was really somewhat more complex than "U=V", is illustrated by its size: if it were printed, it would cover approximately 1 million A4 pages, which makes it probably the longest equation ever used in a mathematical proof.

Stanley’s List

In the end, the work that was spent on the "formulation" was well worth it. With the proof of the Andrews and Robbins conjecture, the scientists have managed to prove the last of a number of famous conjectures, which were presented by US mathematician Richard Stanley at a historic conference in Montreal in 1985. In the years following the conference, all of these conjectures were proved – except for the Andrews and Robbins conjecture. Dr. Kauers comments: "As the last remaining item on Stanley’s list, this conjecture attracted the attention of many experts. Still, it remained unproved for almost thirty years. The proof was finally obtained with an automatic method, which goes to show that modern computer programs can crack mathematical problems where traditional mathematicians fall short."

Granted, such successful results are still an exception. However, this FWF project underscores the potential of computer-based proof. Given the great pace at which computer performance is advancing, such methods will perhaps one day even offer answers to the great unsolved questions in mathematics.

More information: A proof of George Andrews’ and David Robbins’ q-TSPP conjecture. C. Koutschan, M. Kauers D. Zeilberger. DOI:10.1073/pnas.1019186108

Provided by Austrian Science Fund