March 5, 2010 feature
Can a formula predict the outcome of a soccer match?
(PhysOrg.com) -- Soccer, like most sports, is a game full of surprises and lucky or unlucky breaks. After all, if it was easy to predict the winner of a soccer match, there wouldn’t be much reason to watch it. But a team of scientists says that soccer is actually a simple match in statistical terms. To demonstrate, they have derived a function that can predict the expected average outcome of a match in terms of the goal difference between the two competing teams.
In their study, A. Heuer, C. Müller, and O. Rubner, all physicists/chemists from the University of Münster in Germany, have analyzed soccer on a statistical level. As the scientists explain, a soccer match is equivalent to two teams throwing dice. Rolling a 6 means “goal,” and the number of attempts of both teams is fixed at the beginning of the match, reflecting each team’s fitness in that season. The higher its level of fitness, the more chances a team has to score a goal.
How to determine each team’s fitness level is the main task of the scientists’ analysis. To do this, the researchers analyzed data from all soccer matches in the German Bundesliga between the 1977-’78 season and the 2007-’08 season (except for the 1991-’92 season). In this league, every team plays 34 matches per season.
“We attempted to apply typical approaches from the physics community (e.g. analysis of correlation functions, finite-size scaling) to the description of soccer results,” Heuer told PhysOrg.com. “The problem is very similar to the characterization of biased random walks.”
Based on the data, the scientists characterized team fitness as the goal difference within a game averaged over a season (in other words, the difference between number of goals scored and allowed by a team). The scientists’ analysis showed that goal difference is an even bigger influence on team fitness than the number of goals. In addition, based on previous results, the home advantage could be taken into account by a team-independent but season-dependent constant. Overall, the researchers found that a team’s fitness level remains constant throughout the season, although it changes between seasons.
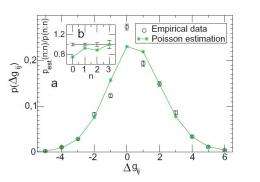
Using team fitness values, the scientists derived a formula to estimate the expected value of the goal difference in a particular match. The actual number of goals in a match (just like rolling dice) could be described as Poissonian processes; the events occur randomly and, for the most part, independently of each other. Taking all analyzed matches into account, the goal distribution determined in this way agrees almost perfectly with the actual data.
“The three key results are (1) the observation of constant team fitness during a season, (2) the derivation of an equation which predicts the average outcome of a match, and (3) the observation that the actual goal distribution can be very well described by a Poisson distribution,” Heuer summarized.
Although the researchers’ equation was accurate in many areas, the researchers found that it became less accurate in cases where the goal difference was one or zero. Specifically, in the real data, there were more zeros (ties) than predicted by the equation, and fewer one-goal differences.
“The agreement with the actual data is perfect within statistical error if analyzing the goals per team,” Heuer said. “[However,] when analyzing the distribution of goal differences, one observes too many draws. This shows that the assumption of independent Poisson processes is not correct in cases where the goal difference is -1, 0, or 1. This points to interesting psychological effects, favoring a draw.”
As the researchers note, there are other random effects that influence goals. These effects include temporary injuries, fatigue, weather conditions that favor one time over another, red cards, and so-called self-affirmative effects - that is, the probability of scoring a goal is increased when a team has already scored one or more goals in that game. Although the influence of these effects is very difficult to predict, the researchers found that these effects have a much smaller overall impact on the final outcome of a match as compared to the typical fitness differences.
The analysis also has interesting effects on how we tend to view soccer matches, according to the researchers. For example, the media will often comment that a team that won or lost played particularly good or bad in that match. In contrast, the results here suggest that a team’s fitness level doesn’t change very much from match to match. Yet media reports (and fans) may have a strong tendency to judge a team’s fitness level based too much on the overall score, while ignoring the random effects that may have actually led to the overall score.
In addition to predicting the outcomes of soccer matches, the analysis could serve as a framework to classify different types of sports in terms of degree of competitiveness. For example, in sports with many points such as basketball, random effects are probably less pronounced, so that the stronger team has a better chance of winning than in sports with low-scoring games.
More information: A. Heuer, C. Muller, and O. Rubner. “Soccer: Is scoring goals a predictable Poissonian process?” Europhysics Letters, 89 (2010) 38007. Doi:10.1209/0295-5075/89/38007
Copyright 2010 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.