Statistical method allows the detection of higher order dependencies

In December, the academic publisher De Gruyter launched its new journal Open Statistics with an opening article by TU Dresden mathematician Dr. Björn Böttcher. The article presents the extension of the statistical measure of distance multivariance developed by Böttcher and his colleagues at TU Dresden.

Distance multivariance is a multivariate dependence measure that can detect dependencies between an arbitrary number of random vectors each of which can have a distinct dimension. In his new article, Böttcher now presents the concept as a unifying theory that combines several classical dependence measures. Connections between two or more high-dimensional variables can be captured and even complicated non-linear dependencies as well as dependencies of higher order can be detected. For numerous scientific disciplines, this method opens up new approaches to detect and evaluate dependencies.

Can the number of missed school days be linked to the age, gender or origin of school students? In a survey of 146 school students, social scientists analyzed various influencing variables on missed school days and examined them for dependencies in order to derive a prediction model. This classic question has already been widely discussed and analyzed with various statistical approaches.

The statistical measure of distance multivariance presents a novel approach to this question: Dr. Björn Böttcher from the Institute of Mathematical Stochastics was able to use distance multivariance to determine the cultural background and a higher order dependence including age and gender as influencing factors for the missed school days. He thus was able to suggest a minimal model. "This is an elementary example for an application of the developed method. I cannot judge whether this is also a substantiated finding with regard to the investigated question. Working with real data and especially the subject-specific interpretation of the results always requires expertise in the respective subject," Dr. Böttcher says, and provides numerous other illustrative examples of the application of his method: "In the paper, I refer to more than 350 freely available data sets from all scientific disciplines in which statistically significant higher-order dependencies occur. Again, whether these dependencies are meaningful in terms of the underlying surveys requires further investigations as well as the expertise in the respective fields," and he adds, "of course, requests for cooperation are always welcome."

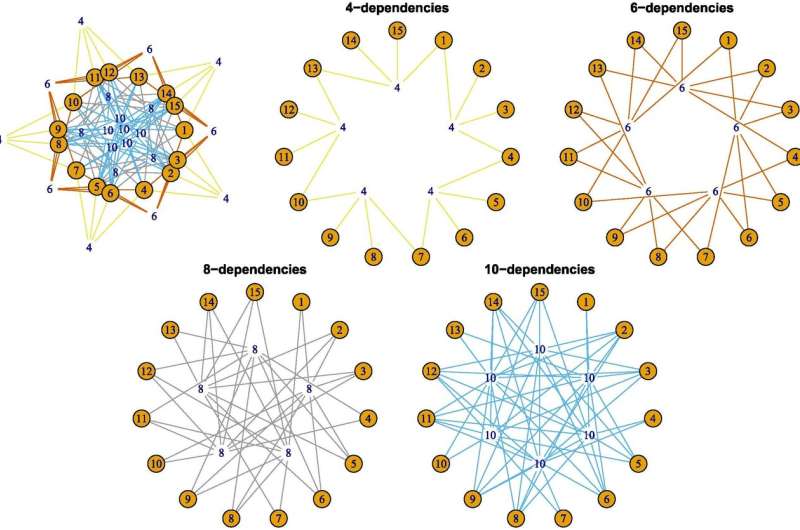
Statistical analysis usually considers dependencies between individual variables. Especially with many variables, it is desirable to remove independent variables prior to studying any specific types of dependence. Dr. Björn Böttcher presents a method for this purpose called "dependence structure detection," which can also be used to detect higher-order dependencies. Variables are called "higher-order dependent" if they are pairwise independent, but more than two variables still influence each other jointly. Dependencies of this kind have not been in the focus of applications so far.

Some scientists suspect that higher-order dependencies occur in genetics in particular: the basic idea here is that several genes together determine a property, but these genes show neither individually any dependence among each other nor individually with the property—thus indeed these would be higher-order dependent. The framework of distance multivariance and the dependence structure detection method are now promising tools for such investigations.

Implementations of the new methods are provided for direct applications in the package "multivariance" for the free statistical computing environment R.