December 31, 2019 feature
Nearly quantized conductance plateau of vortex mode in an iron-based superconductor
![Zero-bias conductance plateau observed on FeTe0.55Se0.45. (A) A schematic of variable tunnel coupling STM/S method. A zero-bias conductance map under 2.0 T is shown on a sample surface. A dI/dV spectrum measured at the center of the vortex core (Vs= -5 mV, It = 500 pA, Vmod = 0.02 mV) is shown in the right-top inset, a sharp zero-bias conductance peak (ZBCP) is observed. When the tunneling current (It) is adjusted by the STM regulation loop, the tunnel coupling between the STM tip and the MZM can be tuned continuously by the tip-sample distance (d). Larger tunnel coupling corresponds to smaller d and larger tunneling-barrier conductance (GN = It/Vs, Vs is the setpoint voltage). Z-offset can be read out simultaneously, which indicates the absolute z-direction motion of the STM tip. (B) A line-cut intensity plot along the dashed white arrow in the inset, measured from the same vortex shown in (A), showing a stable MZM across the vortex core. (C) An overlapping plot of dI/dV spectra under different tunnel coupling values parameterized in GN. The blue curve is measured under the smallest GN while the green curve with the largest GN. (D) A three-dimensional plot of tunnel coupling dependent measurement, dI/dV(E, GN). For clarity, only the data points in the energy range of [-5.0, 0.2] meV are shown. (E) A color-scale plot of (C) within the energy range of [-1.5, 1.5] meV that expands the spectra as a function of GN. The z-offset information, which was taken simultaneously by STM, is also labeled at the upper axis. The maximum distance the tip approached is 3.4 Å. (F) A horizontal line-cut at the zero-bias from (E). The conductance curve shows a plateau behavior with its plateau conductance (GP) equal to (0.64 ± 0.04) G0. (G) Horizontal line-cuts at high-bias values from (E). The absence of a conductance plateau on these curves indicates the conventional tunneling behavior at the energy of continues states. All data are measured at Teff = 377 mK. Credit: Science, doi: 10.1126/science.aax0274 Nearly quantized conductance plateau of vortex mode in an iron-based superconductor](https://scx1.b-cdn.net/csz/news/800a/2019/nearlyquanti.jpg)
When a semiconducting nanowire is coupled to a superconductor, it can be tuned to topological quantum states thought to host localized quasiparticles known as Majorana Zero Modes (MZM). MZMs are their own antiparticles, with promising applications in topological quantum computing. Due to particle-antiparticle equivalence, MZMs exhibit quantized conductance at low temperatures. While many theoretical proposals exist to realize MZMs in solid state systems, their experimental realization is confronted by non-idealities.
In a new report in Science, Shiyu Zhu and a team of interdisciplinary researchers in China and the U.S. used variable-tunnel-coupled scanning tunneling spectroscopy to study tunneling conductance of vortex bound states of superconductors. For instance, superconductors have a "gap" in energy in the absence of electron states—so electrons cannot tunnel in, whereas at a vortex line the magnetic field will close the gap to form electron states. The researchers reported observations with FeTe0.55Se0.45 superconductors, where they recorded conductance plateaus as a function of tunneling coupling for zero-energy vortex bound states, with values close to, and even reaching, the universal quantum conductance value 2e2/h; where e, is the electron charge and h is Planck's constant. In contrast, they did not observe plateaus on either finite energy vortex bound states or within the continuum of electronic states outside the superconducting gap. This behavior of zero-mode conductance supported the existence of MZMs in FeTe0.55Se0.45 crystals.
Majorana Zero Modes (MZMs) obey non-Abelian statistics i.e. excitations beyond the usual fermionic or bosonic modes of excitation, to play an extremely important role in quantum computation. In the past two decades, physicists predicted MZMs within p-wave superconductors and spin-orbit-coupled materials proximitized (to realize properties of a material absent from any constituent region of the heterostructure), by s-wave superconductors. Researchers had observed experimental evidence for MZMs in various systems including semiconductor-superconductor nanowires, topological insulator-superconductor heterostructures and atomic chains on superconducting substrates. Physicists and materials scientists have also recently developed fully gapped bulk iron-based superconductors as a single-material platform to realize MZMs. Subsequently, they found evidence for MZMs in topological vortices on the surface of FeTe0.55Se0.45 crystals using scanning tunneling microscopy/spectroscopy (STM/S).
The conductance of an MZM can exhibit a quantized plateau at sufficiently low temperatures at the value of 2e2/h; where e is the electron charge and h the Planck's constant. This quantized Majorana conductance results from perfect resonant Andreev reflection—a type of particle scattering that occurs at interfaces between a superconductor and normal state material, guaranteed by the inherent particle-hole symmetry of MZM. Scientists had observed a quantized conductance plateau in an InSb-Al nanowire system, consistent with the existence of MZMs. Similarly, iron-based superconductors with zero-bias conductance peaks (ZBCPs) obtained using STM/S experiments have large topological gaps and offer the possibility of observing Majorana quantized conductance, without contamination from low-lying Caroli-de Gennes-Matricon bound states (CBSs). As a result of preceding experimental prospects, Zhu et al. presently employed a variable tunnel coupling STM/S method to study Majorana conductance across a large range of tip-sample distance in vortex cores of FeTe0.55Se0.45 crystal samples.
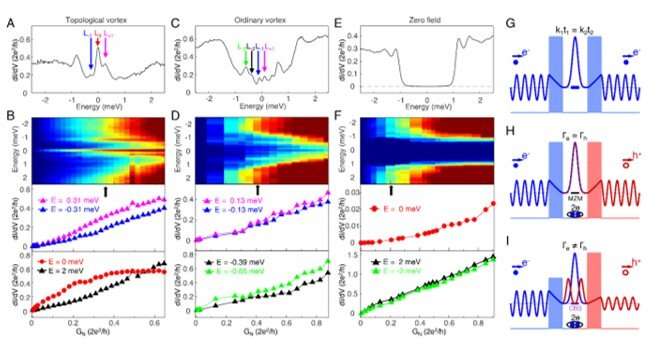
The effective electron temperature of the scanning tunneling microscope (STM) was 377 mK and the researchers continuously tuned the tunnel coupling by changing the tip-sample distance, which correlated with the tunnel-barrier conductance. By applying a 2 T (Tesla) magnetic field perpendicular to the sample surface, Zhu et al. observed a sharp ZBCP (zero-bias conductance peak) at a vortex core. As expected for an isolated MZM in a quantum-limited vortex, the ZBCP did not disperse or split across the vortex core. They performed tunnel-coupling dependent measurements on the observed ZBCP, by adding the STM tip at the center of a topological vortex, to record a set of dI/dV spectra corresponding to the electron density of states at the position of the tip, for different tip-sample distances. They observed the ZBCP to remain as a well-defined peak located at zero energy.
To examine the particle-hole symmetry of the MZMs, they compared and contrasted the conductance behavior of zero-energy MZMs and finite-energy CBSs (Caroli-de Gennes-Matricon bound states). Zhu et al. observed two distinct types of topological and ordinary vortices with, or without MZM, which differed by a half-integer level shift of vortex bound states. They performed tunnel coupling dependent measurements on a topological vortex to show an MZM and first CBS level, at 0 meV and ±0.3 meV, they also conducted measurements on an ordinary vortex.
When the research team repeated the experiments in zero magnetic field at the same location, they observed a hard, superconducting gap. The scientists only observed the conductance plateau feature in ZBCP, which indicated behavior unique to Majorana modes. The plateau behavior observed in the work also provided evidence for the Majorana-induced resonant Andreev reflection. Thereafter, during electron tunneling from a normal electrode through a barrier into a superconductor, the team observed the Andreev reflection process convert the incident electron into an outgoing hole within the same electrode. This resulted in a double-barrier system in the particle-hole Hilbert space (an abstract vector space in quantum mechanics).
In the case of Andreev reflection through a single MZM, equal amplitudes of particle/hole components due to particle-antiparticle equivalence of MZMs ensured identical tunnel coupling, with the electron and hole in the same electrode (Γe = Γh). As a result, the resonant Andreev reflection mediated through a single MZM led to a 2e2/h-quantized zero-bias conductance plateau. In contrast, low-energy CBS and other trivial sub-gap states do not contain Majorana symmetry and the relationship between the electron and hole is broken in a CBS-mediated Andreev reflection, causing an absence of a conductance plateau. Furthermore, when Zhu et al. removed the magnetic field in the experimental system, the observed zero-bias conductance plateau in the vortex core disappeared, therefore the observations could not be credited to quantum ballistic transport.
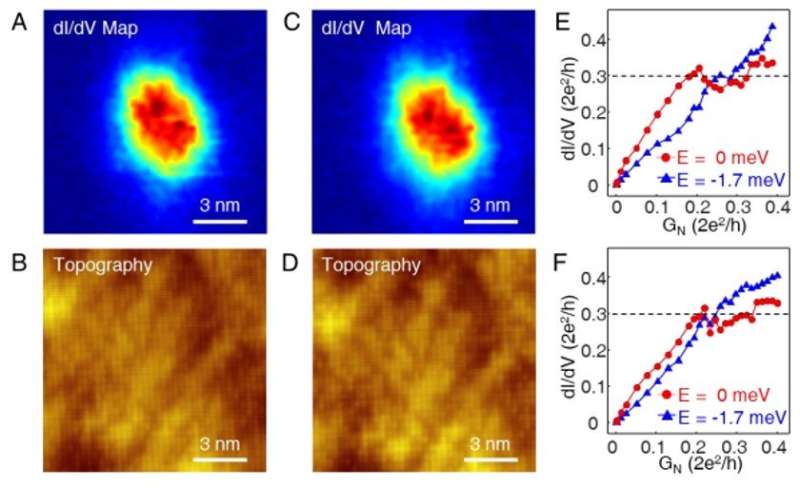
![The conductance variation of Majorana plateau. (A) A histogram of the Gp from 31 sets of data which are measured with the same instrument. Sorting of the plateau conductance (Gp) in the order of increasing magnification can be found (Vs= -5mV, Vmod = 0.02 mV). (B) The overlapping plot of 38 dI/dV spectra selected from a topological vortex that reached a quantized conductance plateau (Vs= -5mV, Vmod = 0.02 mV). (C) A color-scale plot of (B) with the energy range of [-2.5, 2.5] meV that shows the spectra as a function of GN. (D) A horizontal line-cut at the zero-bias from (C). The conductance curve shows the conductance plateau reach G0. (E) A series of tunnel coupling dependent measurements on the same MZM, with four modulation voltages of 0.02 mV, 0.05 mV, 0.10 mV and 0.20 mV. (F) The plot of Gp as a function of modulation voltage of the data shown in (E). (G) Relationship between full-wave half maximum of ZBCP and Gp, obtained from five different MZMs measured at the same experimental conditions, suggesting that the quasiparticle poising effect affects the plateau value. The FWHM were extracted from the spectrum measured at a large tip-sample distance with the same experimental parameters (Vs= -5 mV, It = 500 pA, Vmod = 0.02 mV). Credit: Science, doi: 10.1126/science.aax0274 Nearly quantized conductance plateau of vortex mode in an iron-based superconductor](https://scx1.b-cdn.net/csz/news/800a/2019/2-nearlyquanti.jpg)
The scientists observed the plateau behavior of ZBCPs repeatedly in many topological vortices across 60 measurements. To understand the effects of instrumental broadening on Majorana conductance plateaus, the scientists varied the modulation voltage (Vmod). This allowed them to study the Vmod-evolution of Majorana conductance plateaus on a given topological vortex. Zhu et al. then tested the reversibility of the process by varying tunneling coupling in STM. They found that both topography and the conductance plateau could be reproduced after two repeated sequences to indicate the absence of irreversible damage of the tip and sample during measurements. The research team require further theoretical efforts to gather complete understanding of the experiments, as they did not exclude other mechanisms related to zero-bias conductance plateaus.
In this way, the observation of a zero-bias conductance plateau in an experimental two-dimensional vortex approached the quantized conductance value of 2e2/h. In this work, Shiyu Zhu and colleagues provided spatially-resolved spectroscopic evidence for Majorana-induced resonant electron transmission into a bulk superconductor. The results move a step further toward applications of braiding operators to describe topological entanglements or universal quantum gates for topological quantum computation.
More information: 1. Nearly quantized conductance plateau of vortex zero mode in an iron-based superconductor science.sciencemag.org/content … 2/11/science.aax0274 Shiyu Zhu et al. 12 December 2019, Science.
2. Quantized Majorana conductance www.nature.com/articles/nature26142 Hao Zhang et al. 28 March 2018, Nature.
3. Zero-energy vortex bound state in the superconducting topological surface state of Fe(Se,Te) www.nature.com/articles/s41563-019-0397-1 T. Machida, 17 June 2019, Nature Materials.
Journal information: Science , Nature , Nature Materials
© 2019 Science X Network