October 9, 2017 feature
Scientists address many-electron problem by modeling an infinite chain of hydrogen atoms
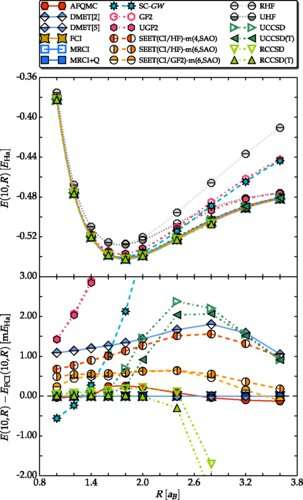
(Phys.org)—For the first time, scientists have determined the equation of state of an infinite chain of hydrogen atoms, which tells the amount of energy each hydrogen atom has, given the bond length between adjacent atoms.
But what is even more interesting for the scientists than the result itself is how they achieved it: by using 20 or so state-of-the-art computational methods that have recently been developed to analyze many-electron systems. The new results offer a first glimpse of what these methods may offer for understanding and predicting the properties of many complex materials, and ultimately designing completely new materials.
The chemists and physicists behind the new study are members of the Simons Collaboration on the Many-Electron Problem, whose ultimate goal is to find methods to model and understand many-electron systems. These are basically any systems that—like an infinite chain of hydrogen atoms— contain large numbers of atoms or molecules, and, therefore, many electrons.
Electron-electron interactions play a large role in determining a material's properties, such as how well it conducts electricity and how hard or soft it is. This information is critical for future initiatives in which researchers design new materials with specific desired properties. Although it's relatively easy to model systems with a few electrons, as the number of electrons grows, the number of possible states that a system can occupy grows exponentially. Modeling such systems then becomes increasingly difficult, since the electron interaction effects are so strong that even the best independent-electron theories break down.
In order to model many-electron systems, researchers have developed several many-electron computational methods that rely on advanced concepts in mathematics and computer science, such as cluster embedding theory, Monte Carlo methods, and tensor networks. But so far, no method exists that can treat all many-electron systems systematically with high accuracy and low computational cost.
In the new study, the scientists used a linear chain of hydrogen atoms as the first benchmark system to test many of these new theoretical methods. By applying approximately 20 of the newest methods to the same problem, the scientists were able to validate and cross-check the results of each method. Although the entire process was computationally complex, it allowed the scientists to combine the strengths of complementary methods and determine the energy per atom to a high degree of accuracy. They could then compare the accuracy of individual methods, which revealed that many of the new methods achieved a high degree of accuracy by themselves.
"There are several facets to this work," Shiwei Zhang, a physics professor at the College of William and Mary and the paper's corresponding author, told Phys.org. "It produced extensive data and comparisons, as a benchmark study was designed to do. It also spurred many algorithmic developments in the different methods, which resulted from the interactions and 'friendly competition.' Perhaps less obvious but most important: it brought people and algorithms together, helped focus the field, and pushed the community to work synergistically in the most productive ways."
The scientists are making the vast amount of data produced in this study available to other researchers, which will soon be available here. They expect that the data will be useful for analyzing the computational methods, benchmarking new methods, studying other many-electron systems, and gaining a deeper understanding of many areas throughout condensed matter physics, quantum chemistry, and materials science, among other fields.
"One short-term goal is to determine the properties of the hydrogen chain," Zhang said. "Surprisingly, even in this relatively simple 'material,' there are important questions for which we do not have definitive answers. We have computed the equation of state. But, for example, what are the electrical and magnetic properties?
"More generally, we would like to expand such benchmark studies to more complex materials. We will continue to develop our computational methods and software. And of course we would like to apply them to tackle the most challenging many-electron problems in molecules and solids important to science and technology."
More information: Mario Motta et al. "Towards the Solution of the Many-Electron Problem in Real Materials: Equation of State of the Hydrogen Chain with State-of-the-Art Many-Body Methods." Physical Review X. DOI: 10.1103/PhysRevX.7.031059
Journal information: Physical Review X
© 2017 Phys.org