Challenging the status quo in mathematics: Teaching for understanding
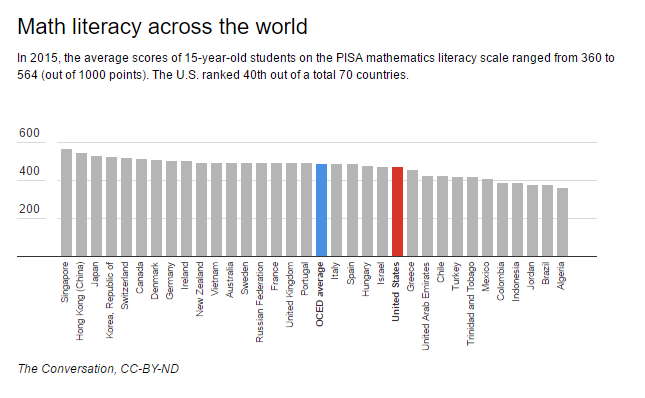
Despite decades of reform efforts, mathematics teaching in the U.S. has changed little in the last century. As a result, it seems, American students have been left behind, now ranking 40th in the world in math literacy.
Several state and national reform efforts have tried to improve things. The most recent Common Core standards had a great deal of promise with their focus on how to teach mathematics, but after several years, changes in teaching practices have been minimal.
As an education researcher, I've observed teachers trying to implement reforms – often with limited success. They sometimes make changes that are more cosmetic than substantive (e.g., more student discussion and group activity), while failing to get at the heart of the matter: What does it truly mean to teach and learn mathematics?
Traditional mathematics teaching
Traditional middle or high school mathematics teaching in the U.S. typically follows this pattern: The teacher demonstrates a set of procedures that can be used to solve a particular kind of problem. A similar problem is then introduced for the class to solve together. Then, the students get a number of exercises to practice on their own.
For example, when students learn about the area of shapes, they're given a set of formulas. They put numbers into the correct formula and compute a solution. More complex questions might give the students the area and have them work backwards to find a missing dimension. Students will often learn a different set of formulas each day: perhaps squares and rectangles one day, triangles the next.
Students in these kinds of lessons are learning to follow a rote process to arrive at a solution. This kind of instruction is so common that it's seldom even questioned. After all, within a particular lesson, it makes the math seem easier, and students who are successful at getting the right answers find this kind of teaching to be very satisfying.
But it turns out that teaching mathematics this way can actually hinder learning. Children can become dependent on tricks and rules that don't hold true in all situations, making it harder to adapt their knowledge to new situations.
For example, in traditional teaching, children learn that they should distribute a number by multiplying across parentheses and will practice doing so with numerous examples. When they begin learning how to solve equations, they often have trouble realizing that it's not always needed. To illustrate, take the equation 3(x + 5) = 30. Children are likely to multiply the 3 across the parentheses to make 3x + 15 = 30. They might just as easily have divided both sides by 3 to make x + 5 = 10, but a child who learned the distribution method might have great difficulty recognizing the alternate method – or even that both procedures are equally correct.
More than a right answer
A key missing ingredient in these traditional lessons is conceptual understanding.
Concepts are ideas, meaning and relationships. It's not just about knowing the procedure (like how to compute the area of a triangle) but also the significance behind the procedure (like what area means). How concepts and procedures are related is important as well, such as how the area of a triangle can be considered half the area of a rectangle and how that relationship can be seen in their area formulas.
Teaching for conceptual understanding has several benefits. Less information has to be memorized, and students can translate their knowledge to new situations more easily. For example, understanding what area means and how areas of different shapes are related can help students understand the concept of volume better. And learning the relationship between area and volume can help students understand how to interpret what the volume means once it's been calculated.
In short, building relationships between how to solve a problem and why it's solved that way helps students use what they already know to solve new problems that they face. Students with a truly conceptual understanding can see how methods emerged from multiple interconnected ideas; their relationship to the solution goes deeper than rote drilling.
Teaching this way is a critical first step if students are to begin recognizing mathematics as meaningful. Conceptual understanding is a key ingredient to helping people think mathematically and use mathematics outside of a classroom.
The will to change
Conceptual understanding in mathematics has been recognized as important for over a century and widely discussed for decades. So why has it not been incorporated into the curriculum, and why does traditional teaching abound?
Learning conceptually can take longer and be more difficult than just presenting formulas. Teaching this way may require additional time commitments both in and outside the classroom. Students may have never been asked to think this way before.
There are systemic obstacles to face as well. A new teacher may face pressure from fellow teachers who teach in traditional ways. The culture of overtesting in the last two decades means that students face more pressure than ever to get right answers on tests.
The results of these tests are also being tied to teacher evaluation systems. Many teachers feel pressure to teach to the test, drilling students so that they can regurgitate information accurately.
If we really want to improve America's mathematics education, we need to rethink both our education system and our teaching methods, and perhaps to consider how other countries approach mathematics instruction. Research has provided evidence that teaching conceptually has benefits not offered by traditional teaching. And students who learn conceptually typically do as well or better on achievement tests.
Renowned education expert Pasi Sahlberg is a former mathematics and physics teacher from Finland. He sums it up well:
"We prepare children to learn how to learn, not how to take a test."
Provided by The Conversation
This article was originally published on The Conversation. Read the original article.![]()