New statistical methods would let researchers deal with data in better, more robust ways

No matter the field, if a researcher is collecting data of any kind, at some point he is going to have to analyze it. And odds are he'll turn to statistics to figure out what the data can tell him.
A wide range of disciplines – such as the social sciences, marketing, manufacturing, the pharmaceutical industry and physics – try to make inferences about a large population of individuals or things based on a relatively small sample. But many researchers are using antiquated statistical techniques that have a relatively high probability of steering them wrong. And that's a problem if it means we're misunderstanding how well a potential new drug works, or the effects of some treatment on a city's water supply, for instance.
As a statistician who's been following advances in the field, I know there are vastly improved methods for comparing groups of individuals or things, as well as understanding the association between two or more variables. These modern robust methods offer the opportunity to achieve a more accurate and more nuanced understanding of data. The trouble is that these better techniques have been slow to make inroads within the larger scientific community.
When classic methods don't cut it
Imagine, for instance, that researchers gather a group of 40 individuals with high cholesterol. Half take drug A, while the other half take a placebo. The researchers discover that those in the first group have a larger average decrease in their cholesterol levels. But how well do the outcomes from just 20 people reflect what would happen if thousands of adults took drug A?
Or on a more cosmic scale, consider astronomer Edwin Hubble, who measured how far 24 galaxies are from Earth and how quickly they're moving away from us. Data from that small group let him draw up an equation that predicts a galaxy's so-called recession velocity given its distance. But how well do Hubble's results reflect the association among all of the millions of galaxies in the universe if they were measured?
In these and many other situations, researchers use small sample sizes simply because of the cost and general difficulty of obtaining data. Classic methods, routinely taught and used, attempt to address these issues by making two key assumptions.

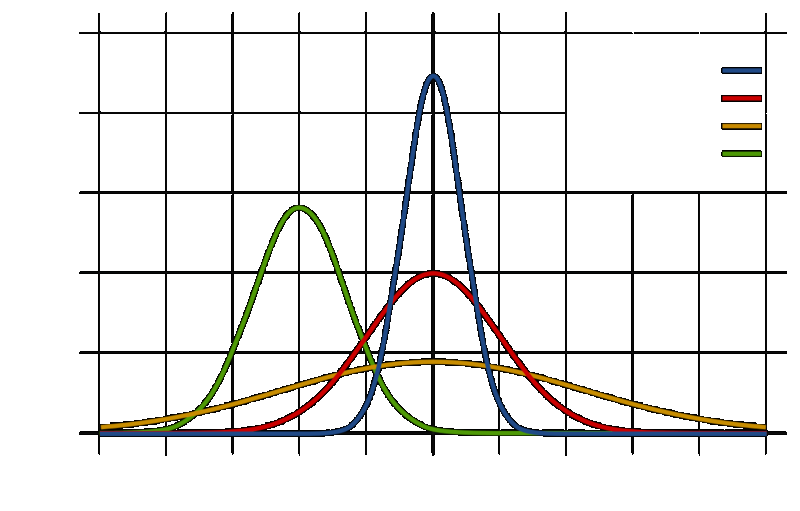
First, scientists assume there's a particular equation for each individual situation that will accurately model the probabilities associated with possible outcomes. The most commonly used equation corresponds to what's called a normal distribution. The resulting plot of the data is bell-shaped and symmetric around some central value.
Second, researchers assume the amount of variation is the same for both groups they're comparing. For example, in the drug study, cholesterol levels will vary among the millions of individuals who might take the medication. Classic techniques assume that the amount of variation among the potential drug recipients is exactly the same as the amount of variation in the placebo group.
A similar assumption is made when studying associations. Consider, for example, a study examining the relationship between age and some measure of depression. Among the millions of individuals aged 20, there will be variation among their depression scores. The same is true at age 30, 80 or any age in between. Classic methods assume that the amount of variation is the same for any two ages we might pick.
All these assumptions allow researchers to use methods that are theoretically and computationally convenient. Unfortunately, they might not yield reasonably accurate results.
While writing my book "Introduction to Robust Estimation and Hypothesis Testing," I analyzed hundreds of journal articles and found that these methods can be unreliable. Indeed, concerns about theoretical and empirical results date back two centuries.
When the groups that researchers are comparing do not differ in any way, or there is no association, classic methods perform well. But if groups differ or there is an association – which is certainly not uncommon – classic methods may falter. Important differences and associations can be missed, and highly misleading inferences can result.
Even recognizing these problems can make things worse, if researchers try to work around the limitations of classic statistical methods using ineffective or technically invalid methods. Transforming the data, or tossing out outliers – any extreme data points that are far out from the other data values – these strategies don't necessarily fix the underlying issues.
A new way
Recent major advances in statistics provide substantially better methods for dealing with these shortcomings. Over the past 30 years, statisticians have solidified the mathematical foundation of these new methods. We call the resulting techniques robust, because they continue to perform well in situations where conventional methods fall down.
Conventional methods provide exact solutions when all those previously mentioned assumptions are met. But even slight violations of these assumptions can be devastating.
The new robust methods, on the other hand, provide approximate solutions when these assumptions are true, making them nearly as accurate as conventional methods. But it's when the situation changes and the assumptions aren't true that the new robust methods shine: They continue to give reasonably accurate solutions for a broad range of situations that cause trouble for the traditional ways.
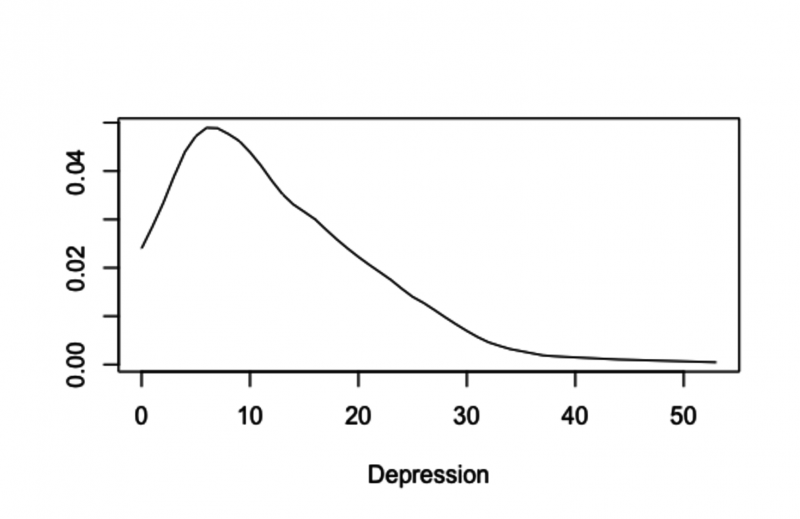
One specific concern is the commonly occurring situation where plots of the data are not symmetric. In a study dealing with depression among older adults, for example, a plot of the data is highly asymmetric – roughly because most adults are not overly depressed.
Outliers are another common challenge. Conventional methods assume that outliers are of no practical importance. But of course that's not always true, so outliers can be disastrous when using conventional methods. Robust methods offer a technically sound – though not obvious, based on standard training – way to deal with this issue that provides a much more accurate interpretation of the data.
Another major advance has been the creation of bootstrap methods, which are more flexible inferential techniques. Combining bootstrap and robust methods has led to a vast array of new and improved techniques for understanding data.
These modern techniques not only increase the likelihood of detecting important differences and associations, but also provide new perspectives that can deepen our understanding of what data are trying to tell us. There is no single perspective that always provides an accurate summary of data. Multiple perspectives can be crucial.
In some situations, modern methods offer little or no improvement over classic techniques. But there is vast evidence illustrating that they can substantially alter our understanding of data.
Education is the missing piece
So why haven't these modern approaches supplanted the classic methods? Conventional wisdom holds that the old ways perform well even when underlying assumptions are false – even though that's not so. And most researchers outside the field don't follow the latest statistics literature that would set them straight.
There is one final hurdle that must be addressed if modern technology is to have a broad impact on our understanding data: basic training.
Most intro stats textbooks don't discuss the many advances and insights that have occurred over the last several decades. This perpetuates the erroneous view that, in terms of basic principles, there have been no important advances since the year 1955. Introductory books aimed at correcting this problem are available and include illustrations on how to apply modern methods with existing software.
Given the millions of dollars and the vast amount of time spent on collecting data, modernizing basic training is absolutely essential – particularly for scientists who don't specialize in statistics. Otherwise, important discoveries will be lost and, in many instances, a deep understanding of the data will be impossible.
Provided by The Conversation
This article was originally published on The Conversation. Read the original article.![]()