Here's what maths can teach us about how to design the perfect car park

There can be few things as frustrating as being stuck in a car park for four hours on a scorching Sunday afternoon; yet this was the unhappy fate of shoppers at a new multi-storey grid car park at an IKEA store in Reading, UK.
The delays were caused by a few factors, including a particularly busy adjacent road, the popularity of the store's opening weekend and the convergence of vehicles on a single exit ramp. Despite the retailer's major £4m investment in constructing good access routes, the infrastructure simply could not cope with the volume of traffic leaving the car park.
#ikeareading @getreading @IKEAUK stuck for 4 hours trying to get OUT of the car park! Nightmare! pic.twitter.com/KyiK4tL3K8
— Peter Coe (@schnoodle27) July 17, 2016
As well as prompting a full-scale investigation by IKEA, such chaos invites us to consider how further gridlock can be prevented. Fortunately, mathematics can provide some basic guiding principles, as we consider how to design the perfect car park.
A numbers game
First, we need to decide how many parking spaces there should be. This is a perennial problem, to which there is no prescriptive answer. Too many spaces are costly and look ugly, while too few spaces result in distraught and dissatisfied customers. Yet some relatively simple maths can help us avoid the worst congestion.
Suppose that daily peak demand averages, say, m cars. We can get a sense of how much the number of cars is likely to vary from the average using standard deviation – let's call this value s. If s is small, it means that the daily peak demand is quite consistent. If s is larger, it means that there's a bit more variation; perhaps attendance spikes on Sundays, or over long weekends, or during sale periods.
Once we know these values, we can use the normal distribution to evaluate the probability that a car park with a given number of spaces will overflow. For example, if m=750 and s=100, then a car park with 800 spaces will overflow on 31% of days, whereas a car park with 1,000 spaces will overflow on only 1% of days. Greater accuracy can be achieved by modifying this simple model to focus on the more extreme events.
While avoiding excess capacity is an important consideration for some organisations, such as airlines, it's better for car parks to err on the side of generosity. While some travellers might be willing to catch later flights in return for compensation, drivers are likely to find the prospect of being redirected to a multi-storey car park two blocks away somewhat less appealing.
The perfect angle
It's also better to err on the side of generosity when it comes to the size of individual parking bays: my own modestly sized vehicle is pitted with craters caused by other doors banging into my side panels.
Bays should leave ample space around the cars to enable pedestrian access and to allow for the axle tracks of turning circles, so that vehicles can enter and exit smartly without cutting the corners of adjacent bays. This can also be achieved with sufficiently wide access lanes, so that cars are parallel to the lines when entering their bays.
Now consider the layout of parking spaces. Assuming that the building has a rectangular plan, there are some simple rules that ensure a convenient and dense population of bays. Rather than having access lanes around the perimeter of each storey, moving the lanes inwards allows us to place bays around the edges and increases the number of spaces.
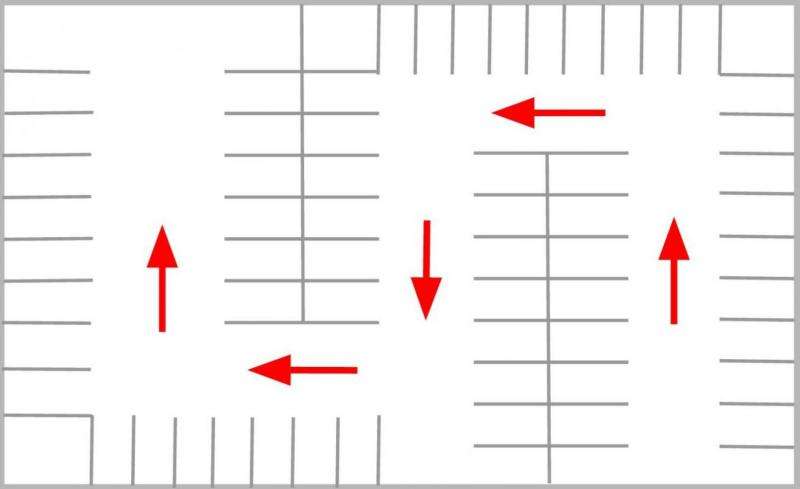
Dead ends are undesirable, as they require drivers to reverse against the flow of traffic, so ramps should be located to avoid these. One-way flow systems throughout the car park also helps to avoid congestion and confusion, while allowing access lanes to be narrower than for a two-way flow of traffic.
A diagonal layout of car parking spaces offers significant advantages over a rectangular layout. Imagine proceeding along an access lane and finding an empty bay. With a rectangular layout you need to change your direction of travel by 90 degrees, which requires a substantial lane width to accommodate your turning circle.
But for a diagonal layout, the bays on both sides are inclined towards you. These require less course adjustment and the access lane can be narrower, so we can fit more parking bays into the same space. For a large car park, a 45 degree bay angle leads to an efficiency saving of 23%. You also need to change your direction of travel much less, so manoeuvring is easier and safer when later reversing out of the bay.
The perfect parking lot
Clearly, there should be at least as many exits as there are entrances. Ramps should be not so steep that they are dangerous for drivers who queue or stall on them. Nor must they be too flat, or they will occupy too much precious space. Other factors are important, including the car wheelbase, ramp length and curvature, and possible transitional ramps.
Isaac Newton's second law of motion – which tells us that that the rate of an object's acceleration depends on the mass of the object, and the magnitude of the force which acts upon it – together with a simple vector diagram, help to balance the car's weight with the slope's normal and frictional forces, to determine acceptable limits for the gradient. One in ten is a generally accepted maximum slope, with lesser gradients often preferred.
If one were to design a new car park from scratch, one of the best of all systems is epitomised by the helical car park design. With one entrance, simple traffic flow and one exit, it is safe for pedestrians and uses the available space efficiently. Crucially, it is also reasonably pretty. Perhaps IKEA should ditch its grid design, and give the helix a whirl.
Source: The Conversation
This article was originally published on The Conversation. Read the original article.
![]()





















