The physics of badminton

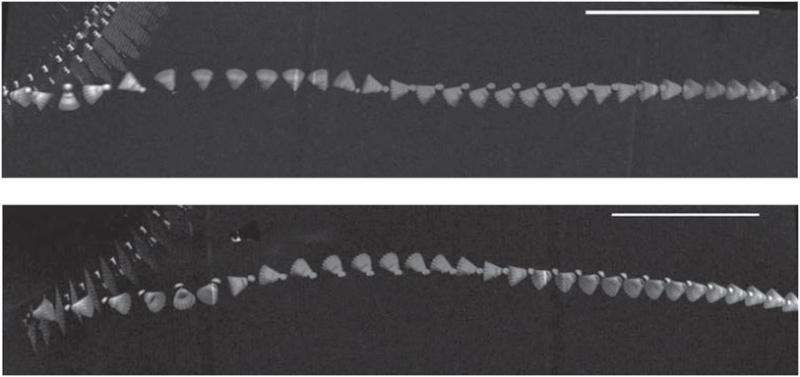
(Phys.org)—When it comes to flying projectiles, the badminton shuttlecock or "birdie" is unusual in that it flips on impact with a racket so that it always flies cork-first. This flipping motion arises from the fact that, unlike almost all other sports projectiles, the shuttlecock has a conical shape and, because the cork is much denser than the feathers, a non-homogeneous mass.

These unique features have inspired extensive research on the physics of shuttlecock trajectories over the years, with one of the latest studies focusing on the flip phenomenon and its implications on game strategies.

The physicists, Caroline Cohen, et al., at Ecole Polytechnique and ESPCI Paris Tech, both in France, have published their paper called "The physics of badminton" in a recent issue of the New Journal of Physics.

For some background, the scientists note that contemporary badminton originated from the Indian game "tomfool." The shuttlecock is traditionally made of 16 goose feathers (or plastic mesh) planted into a cork. It is considered a lightweight and extended object, with a weight of 5 grams and a length of 10 cm, giving it a very large drag. Despite the large drag, shuttlecocks can still achieve top speeds of more than 300 mph (137 m/s).

In their study, the physicists recorded shuttlecock flips using a high-speed video camera. For a typical flip sequence, the footage revealed a 1-millisecond (ms) contact time with the racket, 20 ms for the initial flip, and an 80-ms oscillation time during which the shuttlecock stabilized. When the hit intensity decreases, these times increase. The video also verified the well-known fact that the shuttlecock never performs a full 360° turn.

The scientists also investigated how the shuttlecock geometry influences its flipping dynamics by conducting free fall experiments in a water tank. In particular, they compared shuttlecock prototypes whose feather skirts have different opening angles. They found that opening angles that are too small or too large both result in long flipping and stabilizing times. Not surprisingly, the geometry of real shuttlecocks has been empirically chosen to have intermediate opening angles that allow them to flip and stabilize rapidly.

The researchers also looked at the differences between the trajectories of feathered and plastic shuttlecocks. Experienced players prefer the feathered version because they can be hit at higher speeds without exiting the court, giving the opponent less time to react. By performing tests in wind tunnels, the scientists found that feathered shuttlecocks become more deformed than their plastic counterparts. The larger deformation gives the feather shuttlecocks a more triangular trajectory that contributes to their appeal.

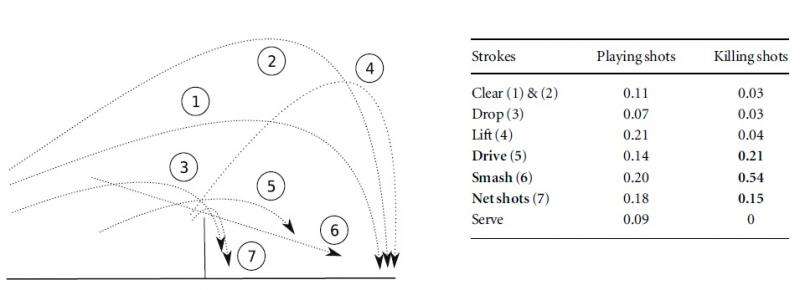
Understanding shuttlecock dynamics also enabled the researchers to propose a classification of different kinds of strokes. They could estimate the probability that each stroke is a "killing shot"—that is, the winning shot that the opponent cannot return. Their analysis showed that shots characterized by certain dynamics are more likely to be killing shots, while other dynamics lend themselves better to preparatory shots.

Many of the shuttlecock's characteristic features stem from one particular trait: its center of mass is about 3 cm in front of its center of pressure (similar to center of mass, center of pressure can be thought of as the point where all of the pressure forces, from the racket and the air, can be considered to have a single point of application). The different centers of mass and pressure cause the shuttlecock to exhibit its unique stabilizing aerodynamic torque and its characteristic flip.

The laws of shuttlecock flights could also apply to other projectiles that have a non-homogeneous mass along their axis, such as air missiles and dandelion seeds or "achenes."

"We particularly looked at the dynamics of a dandelion achene when it falls from the plant," coauthor Baptiste Darbois Texier at Ecole Polytechnique told Phys.org. "Such an object is composed of a dense seed and light 'wings.' When released upside-down, it flips and falls with the seed ahead in the same manner as a shuttlecock. This behavior allows the seed to reach the ground first and give a better chance to lead to a new plant. We showed that the flipping and stabilizing times of a dandelion achene are predicted by the same laws as established for the shuttlecock in our paper."

© 2015 Phys.org