After 400 years, mathematicians find a new class of solid shapes

The work of the Greek polymath Plato has kept millions of people busy for millennia. A few among them have been mathematicians who have obsessed about Platonic solids, a class of geometric forms that are highly regular and are commonly found in nature.
Since Plato's work, two other classes of equilateral convex polyhedra, as the collective of these shapes are called, have been found: Archimedean solids (including truncated icosahedron) and Kepler solids (including rhombic polyhedra). Nearly 400 years after the last class was described, researchers claim that they may have now invented a new, fourth class, which they call Goldberg polyhedra. Also, they believe that their rules show that an infinite number of such classes could exist.
Platonic love for geometry
Equilateral convex polyhedra need to have certain characteristics. First, each of the sides of the polyhedra needs to be of the same length. Second, the shape must be completely solid: that is, it must have a well-defined inside and outside that is separated by the shape itself. Third, any point on a line that connects two points in a shape must never fall outside the shape.
Platonic solids, the first class of such shapes, are well known. They consist of five different shapes: tetrahedron, cube, octahedron, dodecahedron and icosahedron. They have four, six, eight, twelve and twenty faces, respectively.
These highly regular structures are commonly found in nature. For instance, the carbon atoms in a diamond are arranged in a tetrahedral shape. Common salt and fool's gold (iron sulfide) form cubic crystals, and calcium fluoride forms octahedral crystals.
The new discovery comes from researchers who were inspired by finding such interesting polyhedra in their own work that involved the human eye. Stan Schein at the University of California in Los Angeles was studying the retina of the eye when he became interested in the structure of protein called clathrin. Clathrin is involved in moving resources inside and outside cells, and in that process it forms only a handful number of shapes. These shapes intrigued Schein, who ended up coming up with a mathematical explanation for the phenomenon.

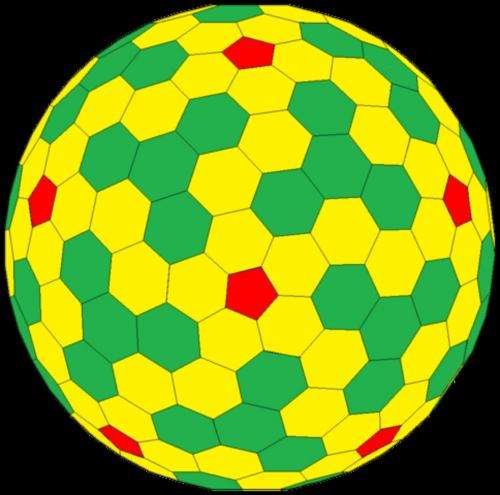
During this work, Schein came across the work of 20th century mathematician Michael Goldberg who described a set of new shapes, which have been named after him, as Goldberg polyhedra. The easiest Goldberg polyhedron to imagine looks like a blown-up football, as the shape is made of many pentagons and hexagons connected to each other in a symmetrical manner (see image to the left).
However, Schein believes that Goldberg's shapes – or cages, as geometers call them – are not polyhedra. "It may be confusing because Goldberg called them polyhedra, a perfectly sensible name to a graph theorist, but to a geometer, polyhedra require planar faces," Schein said.
Instead, in a new paper in the Proceedings of the National Academy of Sciences, Schein and his colleague James Gayed have described that a fourth class of convex polyhedra, which given Goldberg's influence they want to call Goldberg polyhedra, even at the cost of confusing others.
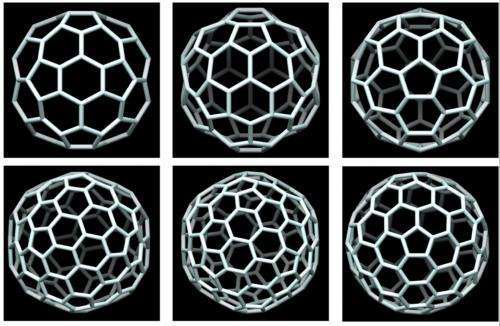
A crude way to describe Schein and Gayed's work, according to David Craven at the University of Birmingham, "is to take a cube and blow it up like a balloon" – which would make its faces bulge (see image to the right). The point at which the new shapes breaks the third rule – which is, any point on a line that connects two points in that shape falls outside the shape – is what Schein and Gayed care about most.
Craven said, "There are two problems: the bulging of the faces, whether it creates a shape like a saddle, and how you turn those bulging faces into multi-faceted shapes. The first is relatively easy to solve. The second is the main problem. Here one can draw hexagons on the side of the bulge, but these hexagons won't be flat. The question is whether you can push and pull all these hexagons around to make each and everyone of them flat."
During the imagined bulging process, even one that involves replacing the bulge with multiple hexagons, as Craven points out, there will be formation of internal angles. These angles formed between lines of the same faces – referred to as dihedral angle discrepancies – means that, according to Schein and Gayed, the shape is no longer a polyhedron. Instead they claimed to have found a way of making those angles zero, which makes all the faces flat, and what is left is a true convex polyhedron (see image below).
Their rules, they claim, can be applied to develop other classes of convex polyhedra. These shapes will be with more and more faces, and in that sense there should be an infinite variety of them.
Playing with shapes
Such mathematical discoveries don't have immediate applications, but often many are found. For example, dome-shaped buildings are never circular in shape. Instead they are built like half-cut Goldberg polyhedra, consisting of many regular shapes that give more strength to the structure than using round-shaped construction material.
However, there may be some immediate applications. The new rules create polyhedra that have structures similar to viruses or fullerenes, a carbon allotrope. The fact that there has been no "cure" against influenza, or common flu, shows that stopping viruses is hard. But if we are able to describe the structure of a virus accurately, we get a step closer to finding a way of fighting them.
If nothing else, Schein's work will invoke mathematicians to find other interesting geometric shapes, now that equilateral convex polyhedra may have been done with.
Source: The Conversation
This story is published courtesy of The Conversation (under Creative Commons-Attribution/No derivatives).
![]()









.jpg)








