At last, how many alien civilizations are there?

During the space age, 1961 was a special year: the Russian cosmonaut Yuri Gagarin became the first man to orbit Earth, while the American astronomer Frank Drake developed the now famous Drake Equation. This equation estimates the number of detectable extraterrestrial civilizations in our Milky Way galaxy, supposing our present electromagnetic detection methods. The Drake equation states:
N = Ns
x fp x ne x fl x fi x fc x fL
N = number of alien civilizations in the Milky Way
Ns = estimated number of stars in the Milky Way;
fp = fraction or percentage of these stars with planets on its orbits;
ne = average number of these planets with potential to host life as we know it;
fl = percentage of these planets that actually develop life;
fi = percentage of these planets that actually develop intelligence on human level;
fc = percentage of these civilizations that actually develop electromagnetic radiation emitting technologies;
fL = percentage of these civilizations that keep emitting electromagnetic signals to space. This factor is extremely dependent on the lifetime a civilization remains electromagnetic communicative.
Looking to the Drake equation factors, it is obvious that none can be precisely determined by modern science. More than that, as we move from the left to right in the equation, estimating each factor becomes more controversial. The later terms are highly speculative, and the values one may attribute to each of them might tell more about a person's beliefs than about scientific facts.
But the Drake equation must not be evaluated only by the numerical values it produces. Some say the Drake equation is a way to organize our ignorance. By exposing the extraterrestrial intelligence hypothesis mathematically, we limit the real possibilities to each term and approach the final answer: how many alien civilizations are there?
The L term is considered the most important one in Drake equation. We have no idea how long a technological civilization can last. Even if only one extraterrestrial civilization lasts for billions of years, or becomes immortal, the L factor would be enough to reduce Drake's equation to N = L. Actually, Frank Drake recognizes this in his license plate: " NEQLSL "
Among dozens of papers written about the Drake Equation, some have suggested new considerations for the formula. One such paper stands out for adding well-established probabilistic principles from statistics. In 2010, the Italian astronomer Claudio Maccone published in the journal Acta Astronautica the Statistical Drake Equation (SDE). It is mathematically more complex and robust than the Classical Drake Equation (CDE).
The SDE is based on the Central Limit Theorem, which states that given the enough number of independent random variables with finite mean and variance, those variables will be normally distributed as represented by a Gaussian or bell curve in a plot. In this way, each of the seven factors of the Drake Equation become independent positive random variables. In his paper, Maccone tested his SDE using values usually accepted by the SETI community, and the results may be good news for the "alien hunters".
Although the numerical results were not his objective, Maccone estimated with his SDE that our galaxy may harbor 4,590 extraterrestrial civilizations. Assuming the same values for each term the Classical Drake Equation estimates only 3,500. So the SDE adds more than 1,000 civilizations to the previous estimate.
Another SDE advantage is to incorporate the standard variation concept, which shows how much variation exists from the average value. In this case the standard variation concept is pretty high: 11,195. In other words, besides human society, zero to 15,785 advanced technological societies could exist in the Milky Way.
If those galactic societies were equally spaced, they could be at an average distance of 28,845 light-years apart. That's too far to have a dialogue with them, even through electromagnetic radiation traveling in the speed of light. So, even with such a potentially high number of advanced civilizations, interstellar communication would still be a major technological challenge.
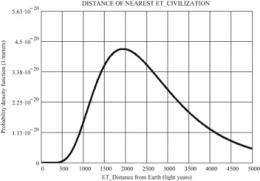
Still, according to SDE, the average distance we should expect to find any alien intelligent life form may be 2,670 light-years from Earth. There is a 75% chance we could find ET between 1,361 and 3,979 light-years away.
500 light-years away, the chance of detecting any signal from an advanced civilization approaches zero. And that is exactly the range in which our present technology is searching for extraterrestrial radio signals. So, the "Great Silence" detected by our radio telescopes is not discouraging at all. Our signals just need to travel a little farther – at least 900 light years more – before they have a high chance of coming across an advanced alien civilization.
Source: Astrobio.net