The secrets of tunneling through energy barriers

As good an electrical conductor at room temperature as copper graphene is, it also outperforms all other known materials as a heat conductor. It is both very dense due to its honeycomb lattice structure and almost completely transparent, making it suitable, among other applications, for touch screens and light panels.

What could partly explain graphene's properties is that electrons travelling inside the material behave as if they were massless. Their behavior is described by the so-called massless Dirac equation that is normally used for high-energy particles such as neutrinos nearing the speed of light. However, electrons in graphene move at a constant speed 300 times smaller than that of light.

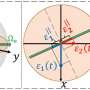
In this review, P.E. Allain and J.N. Fuchs, both from the Université Paris-Sud, focus on the tunneling effect occurring when Dirac electrons found in graphene are transmitted through different types of energy barriers. Contrary to the laws of classical mechanics, which govern larger scale particles that cannot cross energy barriers, electron tunneling is possible in quantum mechanics – though only under restricted conditions, depending on the width and energy height of the barrier.

However, the Dirac electrons found in graphene can tunnel through energy barriers regardless of their width and energy height; a phenomenon called Klein tunneling, described theoretically for 3D massive Dirac electrons by the Swedish physicist Oskar Klein in 1929. Graphene was the first material in which Klein tunneling was observed experimentally, as massive Dirac electrons required energy barriers too large to be observed.

More information: Allain PE, Fuchs JN (2011). Klein tunneling in graphene: optics with massless electrons. European Physical Journal B (EPJ B). DOI 10.1140/epjb/e2011-20351-3

Provided by Springer