May 1, 2007 feature
Scientists find clues to the formation of Fibonacci spirals in nature

While the aesthetics and symmetry of Fibonacci spiral patterns has often attracted scientists, a mathematical or physical explanation for their common occurrence in nature is yet to be discovered. Recently, scientists have successfully produced Fibonacci spiral patterns in the lab, and found that an elastically mismatched bi-layer structure may cause stress patterns that give rise to Fibonacci spirals. The discovery may explain the widespread existence of the pattern in plants.
Chaorong Li, of the Zhejiang Sci-Tech University and the Institute of Physics in Beijing, along with Ailing Ji and Zexian Cao, both of the Chinese Academy of Sciences, produced their Fibonacci spiral pattern by manipulating the stress on inorganic microstructures made of a silver core and a silicon dioxide shell. The spontaneous assembly of Fibonacci patterns has rarely been realized in the laboratory, and the scientists’ results suggest that plant patterns might be modeled by mutually repulsive entities for both spherical and conical surfaces.

“Patterns that evolve naturally are generally an optimized configuration for an assembly of elements under an interaction,” Cao explained to PhysOrg.com. “We conjecture that the Fibonacci spirals are the configuration of least elastic energy. Our experimental results provide a vivid demonstration of this energy principle. This is the best support for this energy principle of phyllotaxis (or “leaf arrangement,” often credited to D'Arcy Thompson) before a rigorous mathematical proof is available.”
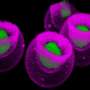
Fibonacci spiral patterns appear in many plants, such as pinecones, pineapples, and sunflowers. The patterns consist of spirals that curve around a surface in both the “sinister” form (clockwise) and the “dexter” form (counterclockwise). The numbers of spirals on a surface are two consecutive numbers in the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, etc.). For example, Li, Ji, and Cao produced a series of spirals of 3x5, 5x8, 8x13, and 13x21. Because their microstructures were very small, the next series (21x34) would have required more than 700 “spherules,” creating so much stress that the structure would break.
In their experiment, the scientists used a technique from stress engineering, which is often used for the mass fabrication of micro- and nanostructures. On an elastically mismatched structure, which consists of a stiff layer on a compliant surface, a variety of buckling occurs. In this example, the scientists heated a mixture of SiO and Ag2O to prepare the silver-cored, silicon-dioxide-shelled microstructures onto substrates at 1270 K, a temperature above the melting point of silver but below that of silicon dioxide, in order to achieve the proper elasticity difference in the subsequent cooling process.
The thermal stress caused the shell to become unstable, and when the conical-shaped structures were cooled, spherules grew on the most stressed sites. The spherules revealed Fibonacci spiral patterns, sometimes growing in the sinister form and sometimes in the dexter form. The scientists couldn’t determine why one form rather than the other would emerge. While the chirality is considered random in plants, Li, Ji and Cao suggested that a geometrical factor may tip the balance.
“Modeled as the least energy configuration on a confining conical support, one element more or less may reverse the chirality,” said Cao. “We are seeking help on this question from simulations.”
The scientists experimented with different shaped structures, and found that only conical shapes produced Fibonacci spirals with definite chirality. On the other hand, spheres produced triangular patterns, while conical shapes with irregularities (such as the shape of a strawberry) produced an ‘X-pattern’. Still, the scientists noted that conical surfaces do not have to be perfect to produce Fibonacci spirals, which may explain the common occurrence in nature.
“The least energy configuration for particles is dependent on the geometry of the space in which the particles are confined—just look at the thorn bundles of various cacti,” Cao explained. “I only know that the Fibonacci spiral patterns are not the least energy pattern for a sphere (try to imagine a football) or flat plane (we can make Fibonacci spirals on street pavement, but it is not self-assembled). However, Fibonacci spirals do appear on conical receptacles in nature. I conjecture that Fibonacci spirals are the least energy configuration on conical supports, but I cannot prove it.”
For plants, Cao’s conjecture is supported even in very old literature, although scientists have yet to discover a mathematical proof. Cao explained why this proof is so difficult.
“The patterns on a sphere are now referred to as the Thomson problem, which has been generalized as the Generalized Riesz Problem,” Cao said. “There is no general method to find the least energy configuration for a given confining geometry, and the numerical solution costs enormous time of both the computers and the scientists. Even worse, it is difficult to make oneself believe that the least energy solution he finds is really the global minimum. And numerical solutions would never be accepted as proof.”
Cao added that there are many similar “embarrassments” in physics. He explained how physicists know that the body-centered cubic lattice is the least energy configuration of atoms for many metals, which is also currently unproven.
“We do wish that one day this will be proven,” he said. ”You know, as David Hilbert once said, ‘Physics is too difficult for physicists.’ In my opinion, a proof of problems of this kind needs new mathematics.”
Citations: Li, Chaorong, Ji, Ailing, and Cao, Zexian. “Stressed Fibonacci spiral patterns of definite chirality.” Applied Physics Letters 90, 164102 (2007).
Li, Chaorong, Zhang, Xiaona, and Cao, Zexian. “Triangular and Fibonacci number patterns driven by stress on core/shell microstructures.” Science 309, 909 (2005).
Copyright 2007 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.