The Mathematics of Natural Motion
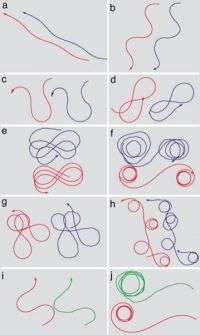
Circles, slaloms, figure eights, and loop-the-loops – biologists studying the motion of Listeria monocytogenes sensed that these paths were related, but they didn’t have a good way to define what fit in and what didn’t. A remarkably simple new mathematical description, published online in the Proceedings of the National Academy of Sciences, reproduces all these shapes with just one pair of equations and only two key variables. Besides helping to identify bacterial mutants, the equations suggest which mechanisms could be driving the motion.
Last winter, Vivek Shenoy, an associate professor of engineering at Brown University, was matched with Julie Theriot, an associate professor at the Stanford School of Medicine, at a biophysics "boot camp" run by Rob Phillips at the California Institute of Technology. Theriot studies Listeria, a disease-causing bacterium that hijacks the actin network of an infected cell to propel itself. Embedded in a network of actin fibers, the bacterium keeps adding actin molecules at its back end, pushing itself forward and leaving behind an actin tail tracing its path.
Those paths intrigued Shenoy as soon as he saw Theriot’s movies of Listeria traveling in the two-dimensional world of a microscope slide. Some bacteria spun in circles, others followed a sine curve, some followed a path like the cloverleaf exchange on a highway. The circles, he thought, were easy to explain. If an actin filament pushed just a bit off center, the bacterium would go in circles, like a swimmer who paddles harder on one side.
With a bit more thought, he cracked the sine curve. What if that off-center point rotated around the axis of motion" When it pushed harder on the right, the bacterium would move to the left; when it pushed to the left of center, the cell would move to the right. If the bacterium moved forward faster than it curved around, a swerving pattern would result.
The clincher came as Shenoy worked out the mathematics to describe this kind of motion. The exact same equation, it turned out, also described the figure-eights, cloverleaves and other looping patterns they had observed. In fact, nearly every time they recorded a new pattern, they found it fit the equation. An equation that can predict observations clearly has a lot going for it, but a mathematical description is not the same thing as a biological mechanism.
"If we can understand things is a simpler setting, such as this one," said Shenoy, "then we can use those insights to study more complex phenomena."
As the team works to fully explain the motion they observe, Shenoy’s equations can narrow the possibilities, ruling out mechanisms that cannot generate both the circular and the spinning component of the motion.
With just two variables – an offset distance and an angle relative to the forward motion – they could reproduce every track they saw, except those produced by mutant microbes that Theriot introduced. The mutants stood out as different. They produced a skidding kind of pattern instead of the graceful curves that most of the bacteria traced.
"The human visual cortex is really good at seeing patterns," said Theriot, "but this gives us a quantitative framework for asking questions that before we could only ask qualitatively."
Being able to pinpoint just how different the mutants are is valuable, said Theriot, because they often are less infectious than normal Listeria. Once Listeria invades a host cell, it uses the actin mechanism to move from cell to cell, never again exposing itself to the organism’s extracellular immune system. A microbe with a deficient movement mechanism is a microbe with less ability to invade neighboring cells.
Link: Abstract
Source: Brown University