New mathematical method provides better way to analyze noise
Humans have 200 million light receptors in their eyes, 10 to 20 million receptors devoted to smell, but only 8,000 dedicated to sound. Yet despite this miniscule number, the auditory system is the fastest of the five senses. Researchers credit this discrepancy to a series of lightning-fast calculations in the brain that translate minimal input into maximal understanding. And whatever those calculations are, they’re far more precise than any sound-analysis program that exists today.
In a recent issue of the Proceedings of the National Academy of Sciences, Marcelo Magnasco, professor and head of the Mathematical Physics Laboratory at Rockefeller University, has published a paper that may prove to be a sound-analysis breakthrough, featuring a mathematical method or “algorithm” that’s far more nuanced at transforming sound into a visual representation than current methods. “This outperforms everything in the market as a general method of sound analysis,” Magnasco says. In fact, he notes, it may be the same type of method the brain actually uses.
Magnasco collaborated with Timothy Gardner, a former Rockefeller graduate student who is now a Burroughs Wellcome Fund fellow at MIT, to figure out how to get computers to process complex, rapidly changing sounds the same way the brain does. They struck upon a mathematical method that reassigned a sound’s rate and frequency data into a set of points that they could make into a histogram — a visual, two-dimensional map of how a sound’s individual frequencies move in time. When they tested their technique against other sound-analysis programs, they found that it gave them a much greater ability to tease out the sound they were interested in from the noise that surrounded it.
One fundamental observation enabled this vast improvement: They were able to visualize the areas in which there was no sound at all. The two researchers used white noise — hissing similar to what you might hear on an un-tuned FM radio — because it’s the most complex sound available, with exactly the same amount of energy at all frequency levels. When they plugged their algorithm into a computer, it reassigned each tone and plotted the data points on a graph in which the x-axis was time and the y-axis was frequency.
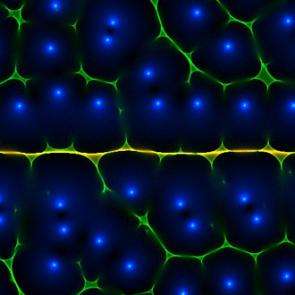
The resulting histograms showed thin, froth-like images, each “bubble” encircling a blue spot. Each blue spot indicated a zero, or a moment during which there was no sound at a particular frequency. “There is a theorem,” Magnasco says, “that tells us that we can know what the sound was by knowing when there was no sound.” In other words, their pictures were being determined not by where there was volume, but where there was silence.
“If you want to show that your analysis is a valid signal estimation method, you have to understand what a sound looks like when it’s embedded in noise,” Magnasco says. So he added a constant tone beneath the white noise. That tone appeared in their histograms as a thin yellow band, bubble edges converging in a horizontal line that cut straight through the center of the froth. This, he says, proves that their algorithm is a viable method of analysis, and one that may be related to how the mammalian brain parses sound.
“The applications are immense, and can be used in most fields of science and technology,” Magnasco says. And those applications aren’t limited to sound, either. It can be used for any kind of data in which a series of time points are juxtaposed with discrete frequencies that are important to pick up. Radar and sonar both depend on this kind of time-frequency analysis, as does speech-recognition software. Medical tests such as electroencephalograms (EEGs), which measure multiple, discrete brainwaves use it, too.
Geologists use time-frequency data to determine the composition of the ground under a surveyor’s feet, and an angler’s fishfinder uses the method to determine the water’s depth and locate schools of fish. But current methods are far from exact, so the algorithm has plenty of potential opportunities. “If we were able to do extremely high-resolution time-frequency analysis, we’d get unbelievable amounts of information from technologies like radar,” Magnasco says. “With radar now, for instance, you’d be able to tell there was a helicopter. With this algorithm, you’d be able to pick out each one of its blades.” With this algorithm, researchers could one day give computers the same acuity as human ears, and give cochlear implants the power of 8,000 hair cells.
Source: Rockefeller University