Yale statistics professor identifies flaws in IOC figure skating scoring system
John W. Emerson, assistant professor of Statistics at Yale, using information found on the web for an exercise in his classroom, examined the results of the recent European Women's Figure Skating Competition and identified a potentially serious flaw in the system for selecting the judging panel.
This competition provided the first complete set of statistics Emerson was able to find from a major competition using the new scoring system.
Emerson had used sports statistics in his classroom in the past -- including writing an article on whether it was a good bet that the University of Connecticut would repeat as the National champion in NCAA Men's Basketball in 2005.
Emerson looked at the standings after the Short Program and compared the recorded standings, based on the actual randomly selected panel of nine out of 12 judges, with the other 219 outcomes of other possible nine-judge panels.
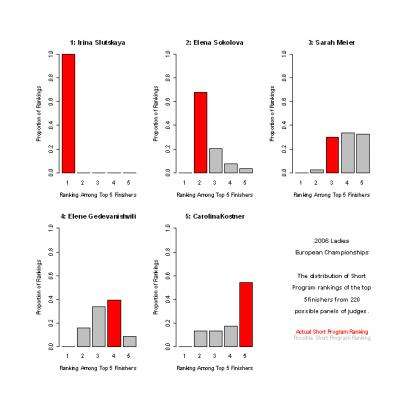
His results showed that in this particular part of the competition, the only ranking within the top five skaters that could not be altered by the random selection of the judging panel was that of the first place skater, Irena Slutskaya.
Further, he points out that only 50 of the 220 possible nine-judge panels would have given the same ranking as the one recorded, but if scoring of all 12 judges was counted, that rank would, in this case, prevail.
Emerson's statement of analysis follows.
The Computer: A Phantom Figure Skating Judge?
John W. Emerson
Torino, Italy, February 11, 2006. During NBC's Prime Time broadcast of the 2006 Olympic competition, commentator Bob Costas discusses the new figure skating "scoring system, designed to increase fairness" � fallout from the judging scandal in Salt Lake City. Two-time gold medal winner Dick Button offers his support of the new system. The viewer is comforted; the integrity of the Olympic Games is intact. Or is it?
Does the new scoring system increase fairness? On some level it does, but the system has introduced the unsettling possibility of dumb luck influencing the medal standings. In a close competition with skaters separated by only a few points, the outcome will likely be determined by a random choice. This is neither desirable nor fair, and the system can easily be improved. The outcome should be determined solely by the skaters and the judges, using the scores of all twelve judges.
For over 100 years, eight judges used the 6.0 standard of scores; the high and low scores were dropped to reduce bias or nationalism in the judging. Judging was not anonymous, and accusations of favoritism were common. The starting order often influenced the scores, with earlier skaters receiving lower scores to "leave room" for the possibility of superior performances later in the session.
In place since the 2004 World Championships and in use at the 2006 Olympic Games, the new system awards points for technical elements as well as five program components: skating skills, transition/linking footwork, performance/execution, choreography/composition, and interpretation.
The scores for the technical elements depend on a base value for the level of difficulty of the elements. The twelve judges add or deduct points from this base value, acknowledging the "grade of execution" of the performance of the elements. Program component scores range from 0 to 10, with increments of 0.25, reflecting the overall presentation of the program and quality of the figure skating.
Judging is now anonymous. Nine of twelve judges are selected at random for the Short Program and again for the Free Skate. Scores for each executed element or program component are calculated using a trimmed mean, as in the old system, dropping the maximum and minimum of the nine scores.
Random elimination of three judges results in 220 possible combinations of nine-judge panels. However, only one panel actually determines the outcome. An examination of the Ladies' 2006 European Figure Skating Championships illustrates the problem.
The Short Program was a close competition between four of the top five skaters: Irina Slutskaya (66.43), Elena Sokolova (60.88), Sarah Meier (60.87), Elena Gedevanishvili (60.19), and Carolina Kostner (60.04). The scores were calculated after a computer randomly excluded judges 4, 6, and 11, whose identities and nationalities are unknown.
Only 50 of the 220 possible panels would have resulted in the same ranking of the skaters following the Short Program. Scores calculated using all of the twelve judges would have resulted in the same ranking, but with slightly different numerical scores.
Random elimination of a different set of judges could have radically changed these standings. Only Slutskaya's standing was secure; each of the other skaters could have placed as high as 2nd or as low as 5th in the Short Program. If the scores had been similarly close following the Free Skate (they were not, fortunately), the medal standings would have been determined by the random selection of the panels of judges.
The following graphs show the distribution of Short Skate rankings for each of the top 5 finishers, based on 220 possible panels of judges. Each of these panels awarded the highest score to Slutskaya. Meier was particularly lucky: while she placed 3rd, more than half of the possible panels would have placed her in 4th or 5th position. Conversely, Gedevanishvili, who placed 4th, was particularly unlucky � more than half of the possible panels would scored her in 2nd or 3rd position. Even Kostner, in 5th place, would have been ranked 2nd or 3rd by about one-third of the panels.
Imagine a similarly close competition for the Olympic medals in Torino, Italy.
I hope I never have to hear a 4th or 5th place finisher give the following interview: "I did my best, and I would have won Bronze if all twelve judges' scores had been included. And if a different panel of 9 judges had been selected, I might have won Gold."
We can only hope that the podium in Torino on February 23 will be determined by the judging of the skaters on the ice. Not by a computer.
Source: Yale University