Mathematicians solve old problem that may have new applications
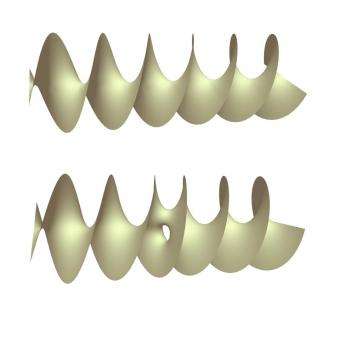
A twisted soap bubble with a handle? If you find that hard to visualize, it's understandable. Experts had thought for more than 200 years that such a structure was not even mathematically possible. But no longer.
In a paper published in the Nov. 15 issue of Proceedings of the National Academy of Sciences, mathematicians Matthias Weber of Indiana University, David Hoffman of Stanford University, and Michael Wolf of Rice University presented a proof of the existence of a new minimal surface they call a genus one helicoid.
"This proof tells us that our intuition was not quite right about what is possible and what is not possible," Weber said. "Probably one reason it was not discovered sooner is that no one imagined that something like this could exist."
A helicoid is what results when one of the simplest shapes -- a flat plane -- is twisted an infinite number of times. If the helicoid is vertical, its shape resembles a spiral parking ramp.
The new surface looks much like this traditional helicoid with an extra feature: a handle such as one finds on a coffee mug. It turns out that on one "floor" of the parking ramp there is an additional column -- the handle.
All minimal surfaces have something important in common: a minimal surface area.
"A minimal surface is formed when the pressure on both sides of a surface is the same," Weber explained. "'For example, when you dip a bent coat hanger into soapy water, the soap bubble that forms on the hanger is a minimal surface." These soap bubbles can have various shapes, depending on the shape of the coat hanger, but in every case the bubble is trying to minimize surface tension, he said. This happens when the bubble has the smallest possible surface area.
At every point, a minimal surface is either flat or shaped like a saddle or a potato chip.
Minimal surfaces are proving to be important at the molecular level. "Minimal surfaces actually occur in nature at the nanoscale as interfaces between certain substances," Weber said. An example is some copolymers that are plastics used to make new kinds of fabrics. When these copolymers are mixed, there are interfaces between them that are minimal surfaces. Knowing what these interfaces look like can help in determining what the chemical properties of the mixture will be.
Minimal surfaces are extremely stable as physical objects, Weber pointed out, and this can be an advantage in many kinds of structures. He has heard from architects who have seen computerized illustrations of some of his minimal surfaces and are intrigued by the possibility of adapting them to structures, both interior and exterior. He has exchanged information about minimal surfaces with some architects and is exploring ways to collaborate with them.
Calendars are another use for this work, highlighting the aesthetic qualities of minimal surfaces. These aesthetic qualities are on vivid display in Weber's computer gallery of minimal surfaces at www.indiana.edu/~minimal/gallery/index/index.html , which shows minimal-surface objects set in imaginary landscapes.
"The images in the gallery are not intended as illustrations of mathematical facts," Weber said. "They more than fulfill their purpose if people see them and can feel some of the intriguing enchantment that a mathematician feels when exploring the mathematical objects."
In a second gallery at www.indiana.edu/~minimal/archive/index.html the pictures do illustrate mathematical facts. "This is the most comprehensive collection of minimal surfaces available," Weber said. "Users can download programs that recreate the surfaces, allowing them to conduct numerical and visual experiments."
The mathematicians' complete proof is more than 100 pages long. The abstract of their report in Proceedings of the National Academy of Sciences is available at www.pnas.org/cgi/content/abstract/102/46/16566 .
Source: Indiana University