February 25, 2014 feature
Spatial order increases cooperation in quantum prisoner's dilemma game

Although we know that cooperating with others usually brings about the best results for everyone, oftentimes being uncooperative can be more beneficial to an individual who takes advantage of others who do cooperate. One of the most well-known tools for investigating cooperation is the prisoner's dilemma game, in which players receive different pay-offs depending on whether they and their partner decide to cooperate or not. In this game, a player receives the highest pay-off when she chooses to defect while her partner all-too-trustingly cooperates, and consequently receives the lowest pay-off.
In a new study, Ramón Alonso-Sanz, a researcher at the Technical University of Madrid, has developed and analyzed a spatial formulation of a quantum version of the prisoner's dilemma game. He found that spatial order increases cooperation compared with the original version of the game.
"Cooperation is not a 'rational' choice in the simple prisoner's dilemma game," Alonso-Sanz told Phys.org. "Thus, whatever mechanism that may help to explain the persistence of cooperation is always celebrated."
The game is played on a grid—or "cellular automaton"—with multiple players. There are two types of players, A and B, who alternately occupy the spaces of the grid like white and black spaces on a checkerboard.
Each player interacts only with his four adjacent partners (up, down, left, and right), all of whom are the opposite type of player as him. In each round, a player's pay-off is the sum of the pay-offs from these four interactions. (Pay-offs are 5, 4, 2, and 1 for DC, CC, DD, and CD, respectively, where C = cooperation and D = defection, with the first letter representing the player's choice and the second letter representing the choice of his partner.)
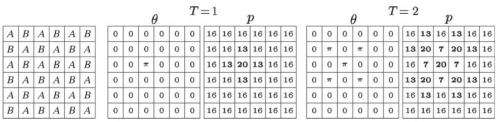
In the next round, the player adopts the strategy used by the most successful of the four players in the spaces diagonal to him (all of whom are the same type as him) or his own strategy—whichever received the highest pay-off in the previous round. Following this "imitation of the best" strategy, the game evolves over multiple iterations.
When Alonso-Sanz performed classical simulations of this spatial prisoner's dilemma game, he found that defection spread quickly. Even when beginning the game with a scenario where all but one A player chose to cooperate, the results showed that that one player's choice to defect spread to all of the other A players. In a 6x6 grid, every A player chose defection after only four iterations of the game.
But the game evolves very differently when quantum entanglement is incorporated. When players can use quantum strategies, a player's defective choice does not spread through the game space, even though it may offer the highest payoff. This is because quantum entanglement changes the probabilities of the pay-offs. Whereas defection spreads in the classical version of the game, in the quantum version defection actually fades and instead mutual cooperation among all players emerges.
"The parameter pay-offs (e.g., 5,4,2,1) are of course unaltered," Alonso-Sanz explained. "What varies are the accessible probabilities, and consequently the mean (or expected) payoffs."
Although intriguing, this difference between the classical and quantum versions of the prisoner's dilemma game is not unexpected. In 1999, researchers found that classical and quantum formulations of the prisoner's dilemma game have different pairs of strategies that are in Nash equilibrium, meaning that the strategies of both players are the best response to one another. In the classical version, mutual defection is the only pair of strategies in Nash equilibrium. Even though both players would receive a larger payoff if they both cooperated, mutual cooperation is not a pair of strategies in Nash equilibrium because either player could do better for herself by choosing to defect.
However, in the quantum version, mutual cooperation is in Nash equilibrium. That is, when two players both choose cooperation, neither player can do better by choosing to defect instead. The current study demonstrates how this equilibrium easily emerges in a spatial formulation of the prisoner's dilemma game.
By making some modifications to the game, Alonso-Sanz found some other interesting results. In an unfair situation in which A-type players can use quantum strategies but B-type players are restricted to classical strategies, the A players rapidly take advantage of the B players. However, when the quantum A players are given a memory and forced to take into account the outcomes of several previous iterations, they actually choose worse strategies than the classical B players. This game results in both kinds of players receiving lower pay-offs than they would otherwise receive.
Overall, the results here are similar to the results from Alonso-Sanz's previous work on a game called Battle of the Sexes, which deals with coordination. As in the case of the prisoner's dilemma, a quantum formulation of the spatial Battle of the Sexes game evolves in a manner notably distinct from that of its classical counterpart: specifically, it leads to a more homogeneous distribution of coordination rather than clusters of coordination. Within the context of these spatially formulated quantum games, researchers may better understand how cooperation and coordination materialize in a society of competitive individuals.
More information: Ramón Alonso-Sanz. "A quantum prisoner's dilemma cellular automaton." Proceedings of The Royal Society A. DOI: 10.1098/rspa.2013.0793
Ramón Alonso-Sanz. "On a three-parameter quantum battle of the sexes cellular automaton." Quantum Information Processing. DOI: 10.1007/s11128-012-0496-2
Ramón Alonso-Sanz. "A quantum battle of the sexes cellular automaton." Proceedings of The Royal Society A. DOI: 10.1098/rspa.2012.0161
© 2014 Phys.org. All rights reserved.