Understanding how a cell becomes a person, with math

We all start from a single cell, the fertilized egg. From this cell, through a process involving cell division, cell differentiation and cell death a human being takes shape, ultimately made up of over 37 trillion cells across hundreds or thousands of different cell types.

While we broadly understand many aspects of this developmental process, we do not know many of the details.

A better understanding of how a fertilized egg turns into trillions of cells to form a human is primarily a mathematical challenge. What we need are mathematical models that can predict and show what happens.

The problem is we don't have one—yet.

In engineering, mathematical and computer modeling are now crucial—an airplane is tested in computer simulations long before the first prototype is even built. But biotechnology still largely relies on a combination of trial and error—and serendipity—to come up with new treatments and therapies.

So, this lack of mathematical models is a major bottleneck for biotechnology. But the fledgling discipline of synthetic biology, where a mathematical model would be extremely useful in understanding the potential effectiveness of new designs is crucial—whether for drugs, devices or synthetic tissues.

This is why mathematical models of cells, especially of whole cells, are widely regarded as one of the grand scientific challenges of this century.

But are we making progress? The short answer is yes, but we are sometimes having to look backwards to go forwards.

In the 1950s, British biologist and mathematician Conrad Hal Waddington described cell development as a marble rolling down a hilly landscape. The valleys correspond to cells becoming types—skin, bone, nerve cells—and the hills dividing the valleys correspond to junctures in the developmental process, where the fate of a cell is chosen.

By the time the marble comes to rest in the bottom of the valley, it has become a specialized cell with a defined function.

"Choice" here is a vague term and refers to the multitude of intracellular molecular processes that underly cellular function and behavior.

In humans, some 22,000 genes and their products could affect cellular dynamics. In comparison, in bacteria the number of genes is much smaller—Escherichia coli, the most important bacterial model organism, has about 4,500 genes that affect how this cell responds to the environment.

The landscape of hills and valleys described by Waddington tries to summarize and simplify the concerted action of these thousands of genes, which affect the shape, the bumpiness, the number of valleys and hills and other aspects of the landscape.

Now it turns out that Waddington's landscape is more than just a metaphor. It can be linked to mathematical descriptions.

We identify the valley bottoms with stable states: left to its own devices, the marble (or undifferentiated cell) located at the valley bottom will stay there forever. But if the marble is poised on a hilltop, even a slight disturbance will lead to it running down the slope into a particular valley.

Mathematicians in the 1970s took the valley concept and developed a branch of mathematics, with the evocative name "catastrophe theory."

This theory considers how highly fertilized mathematical "landscapes" can change, and any qualitative change is called a "catastrophe," or in less emotive language a "singularity."

Fifty years later, mathematicians and computational scientists have rediscovered these landscape models in completely new applications.

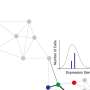
Because we can now measure gene expression (or activation) in single cells, we can see that the internal molecular processes are like cells traversing a hilly landscape.

So, we can now connect the landscape model with experimental data in a way that Waddington could only dream of.

Linking the activity of genes to the landscape model has become an active and exciting area of research. We hope to use this to understand how cells move across this landscape, from a single fertilized egg cell to thousands of fully differentiated cell types in an adult human.

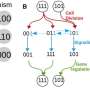
One problem that has received little attention is how the randomness (or noise) of molecular processes inside cells affects the landscape and the dynamics of cells on the landscape.

This is at the heart of our recent research published in Cell Systems, where we explore how this molecular noise can profoundly affect the dynamics. Our research team, supported by an ARC Australian Laureate Fellowship, aims to develop an approach that incorporates randomness into a system that can control and shape the landscape.

In landscape terminology, molecular noise can move valleys and hills—it can even make valleys disappear or form new valleys and hills, changing the direction while adding or removing potential destinations of our metaphorical marble.

If we translate this back into the language of biology, this means that cell types that could exist in noise-less (or low-noise) systems can disappear once noise affects the system, and vice versa.

Noise matters.

It's not merely an inconvenience or nuisance—noise affects the types of cells that can exist in an organism. The hope is that we can use the growing amount of single-cell molecular data, and couple this with mathematical models that consider both the intricate dynamics of gene regulation and cellular processes, as well as the effects of noise.

Our ultimate aim is to develop a complete mathematical model of biological cells.

So far, we have a mathematical model for just one cell type (out of 100 million or so), the tiny bacterium Mycoplasma genitalium, that allows us to study and make testable predictions about its behavior.

This is now changing through the work of mathematical and computational biologists.

Our research group is collaborating with researchers around the world to tackle the complex, but we believe achievable, goal of modeling any cell type, including the multitude of human cells.

One of the key insights that give us this confidence is that biology uses and reuses very similar molecular mechanisms across the whole tree of life.

Our descent from a shared common ancestor is one of the fundamental principles in biology, and we can exploit this to make our work easier: once we have a model for one organism, the next one will be easier to model, and so forth.

The evolutionary relationships between species mean we can borrow insights from other species. And in a multicellular organism, where all cells are derived from a single fertilized egg, we can borrow insights from other cell types as we fill in the gaps in our organism models.