Artificial intelligence reduces a 100,000-equation quantum physics problem to only four equations

Using artificial intelligence, physicists have compressed a daunting quantum problem that until now required 100,000 equations into a bite-size task of as few as four equations—all without sacrificing accuracy. The work, published in the September 23 issue of Physical Review Letters, could revolutionize how scientists investigate systems containing many interacting electrons. Moreover, if scalable to other problems, the approach could potentially aid in the design of materials with sought-after properties such as superconductivity or utility for clean energy generation.
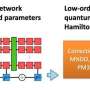
"We start with this huge object of all these coupled-together differential equations; then we're using machine learning to turn it into something so small you can count it on your fingers," says study lead author Domenico Di Sante, a visiting research fellow at the Flatiron Institute's Center for Computational Quantum Physics (CCQ) in New York City and an assistant professor at the University of Bologna in Italy.
The formidable problem concerns how electrons behave as they move on a gridlike lattice. When two electrons occupy the same lattice site, they interact. This setup, known as the Hubbard model, is an idealization of several important classes of materials and enables scientists to learn how electron behavior gives rise to sought-after phases of matter, such as superconductivity, in which electrons flow through a material without resistance. The model also serves as a testing ground for new methods before they're unleashed on more complex quantum systems.
The Hubbard model is deceptively simple, however. For even a modest number of electrons and cutting-edge computational approaches, the problem requires serious computing power. That's because when electrons interact, their fates can become quantum mechanically entangled: Even once they're far apart on different lattice sites, the two electrons can't be treated individually, so physicists must deal with all the electrons at once rather than one at a time. With more electrons, more entanglements crop up, making the computational challenge exponentially harder.
One way of studying a quantum system is by using what's called a renormalization group. That's a mathematical apparatus physicists use to look at how the behavior of a system—such as the Hubbard model—changes when scientists modify properties such as temperature or look at the properties on different scales. Unfortunately, a renormalization group that keeps track of all possible couplings between electrons and doesn't sacrifice anything can contain tens of thousands, hundreds of thousands or even millions of individual equations that need to be solved. On top of that, the equations are tricky: Each represents a pair of electrons interacting.
Di Sante and his colleagues wondered if they could use a machine learning tool known as a neural network to make the renormalization group more manageable. The neural network is like a cross between a frantic switchboard operator and survival-of-the-fittest evolution. First, the machine learning program creates connections within the full-size renormalization group. The neural network then tweaks the strengths of those connections until it finds a small set of equations that generates the same solution as the original, jumbo-size renormalization group. The program's output captured the Hubbard model's physics even with just four equations.
"It's essentially a machine that has the power to discover hidden patterns," Di Sante says. "When we saw the result, we said, 'Wow, this is more than what we expected.' We were really able to capture the relevant physics."
Training the machine learning program required a lot of computational muscle, and the program ran for entire weeks. The good news, Di Sante says, is that now that they have their program coached, they can adapt it to work on other problems without having to start from scratch. He and his collaborators are also investigating just what the machine learning is actually "learning" about the system, which could provide additional insights that might otherwise be hard for physicists to decipher.
Ultimately, the biggest open question is how well the new approach works on more complex quantum systems such as materials in which electrons interact at long distances. In addition, there are exciting possibilities for using the technique in other fields that deal with renormalization groups, Di Sante says, such as cosmology and neuroscience.
More information: Domenico Di Sante et al, Deep Learning the Functional Renormalization Group, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.129.136402
Journal information: Physical Review Letters
Provided by Simons Foundation