How to explain localized gap modes in Bose-Einstein condensates
Bose-Einstein condensates (BECs), created in ultracold bosonic atoms and degenerate quantum gases, are a macroscopic quantum phenomenon and are considered as a single particle in mean-filed theory. By preparing the BECs or ultracold atomic gases onto optical lattices, the existence of nonlinear matter-wave solitons and their dynamics and simulation in condensed-matter physics can be investigated.
However, for the ultracold atomic system under the mean-field approximation and under the many-body interaction, the matter-wave solitons in high dimensions are difficult to evolve stably due to the critical collapse and supercritical collapse.
In a study published in Advanced Photonics Research, a research team led by Prof. Zeng Jianhua from the Xi'an Institute of Optics and Precision Mechanics (XIOPM) of the Chinese Academy of Sciences (CAS) theoretically explored the issue of overcoming the supercritical collapse for three-dimensional matter-wave solitons.
In addition to optical lattice techniques, Feshbach resonances can also tune the collisional interaction between the atoms, thereby providing a nonlinear modulation approach for the study of localized matter waves and many-body physical phenomena.
The combination of linear lattice and nonlinear lattice has the characteristics of spatial structure resonance and non-resonance, which provides a more flexible, diverse and easily controllable means for the study of matter wave localization and quantum simulation.
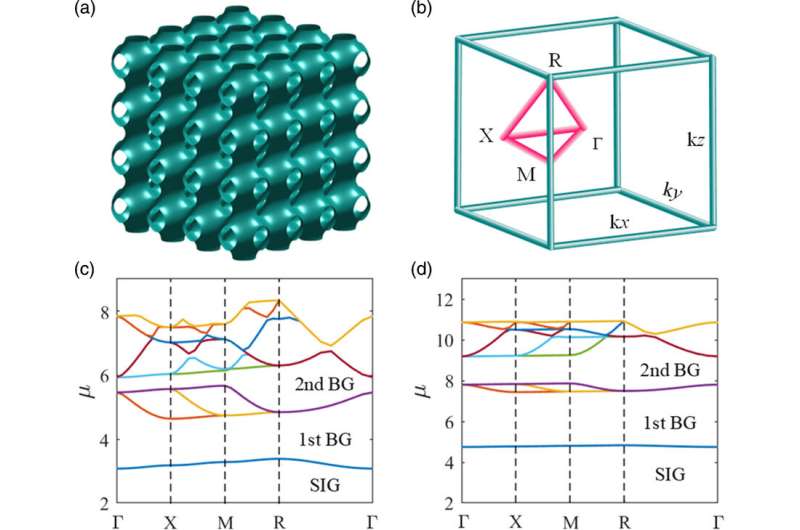
According to the researchers, they were inspired by previous works to investigate the generation and dynamic stability of various types of three-dimensional nonlinear matter-wave localized gap modes in BECs by combining the three-dimensional optical lattice technology with periodic nonlinear Feshbach resonance technology.
The researchers found that all the three-dimensional localized gap modes are extremely stable only in the middle part of the linear bandgap spectrum, and are extremely unstable at the edge of the bandgap spectrum, exhibiting rich dynamic properties.
The research results reveal the nonlinear mechanism of three-dimensional localized bandgap modes in high-dimensional space.
More information: Jiawei Li et al, 3D Nonlinear Localized Gap Modes in Bose‐Einstein Condensates Trapped by Optical Lattices and Space‐Periodic Nonlinear Potentials, Advanced Photonics Research (2022). DOI: 10.1002/adpr.202100288
Provided by Chinese Academy of Sciences