January 4, 2022 feature
Experimental quantum teleportation of propagating microwaves
The field of experimental quantum communication promises ways of efficient and unconditional secure information exchange in quantum states. The possibility of transferring quantum information forms a cornerstone of the emerging field of quantum communication and quantum computation. Recent breakthroughs in quantum computation with superconducting circuits trigger a demand for quantum communication channels between superconducting processors separated in space at microwave length frequencies. To pursue this goal, Kirill G. Fedorov, and a team of scientists in Germany, Finland and Japan demonstrated unconditional quantum teleportation to propagate coherent microwave states by exploring two-mode squeezing and analog feedforward across a distance of 0.42 m. The researchers achieved a teleportation fidelity of F= 0.689±0.004, which exceeded the asymptotic no-cloning threshold, preventing the use of classical error correction methods on quantum states. The quantum state of the teleported state was preserved to open the avenue towards unconditional security in microwave quantum communication.
Quantum teleportation (QT).
The promise of quantum communication is based on the delivery of efficient and unconditionally secure ways to exchange information by exploring the quantum laws of physics. Quantum teleportation (QT) is an exemplary protocol that stands out to allow the disembodied and safe transfer of unknown quantum states using quantum entanglement and classical communication as resources. Recent progress in quantum computation with superconducting circuits has led to quantum communication between spatially separated superconducting processes functioning at microwave length frequencies. Methods to achieve this communication task includes the propagation of two-mode squeezed (TMS) microwaves to entangle remote qubits and teleport microwave states to interface between remote superconducting systems. Fedorov et al. demonstrated the deterministic QT of coherent microwave states by exploring two-mode squeezing and analog feedforward across a distance of 0.42 m to provide a key feature for future microwave quantum local area networks and modular quantum computing.
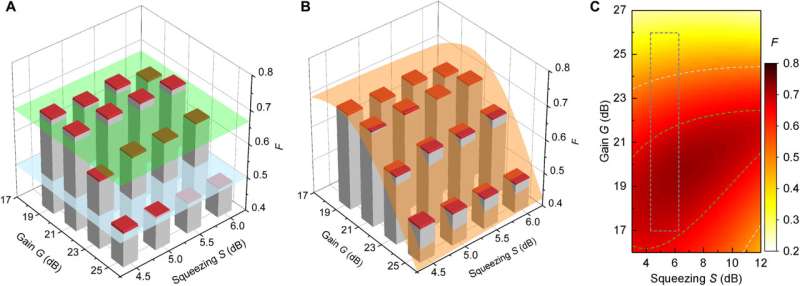
Transport of an unknown quantum state
The process of quantum computing aims to achieve the classically impossible goal of transferring an unknown quantum state from one place to another without direct transfer. The task is typically quantified with a known teleportation fidelity to express the overlap in the phase space between an unknown input state and a teleported output state. By exceeding the classical fidelity threshold, researchers can thereby experiment transitions to the quantum realm via nonclassical correlations such as quantum entanglement. The precise value of the classical fidelity threshold is a subject of many scientific discussions depending on the teleported states and the respective Hilbert space dimension (the dimensional analysis of communication through a quantum channel). For instance, the value for a specific task of teleporting coherent quantum states that differs from the threshold for qubit states can be experimentally overcome with superconducting qubits. Furthermore, the teleportation of continuous-variable Gaussian states has many technical advantages compared with discrete variable states, where the experimental generation and control of weak coherent tones are significantly due to their origin from conventional microwave generators. Researchers can generate continuous-variable entangled states, in the form of two-mode squeezed light via weakly nonlinear superconducting devices including various Josephson parametric devices, to generate deterministic entanglement for higher communication bit rates compared to the frequently used non-deterministic entanglement generation schemes.
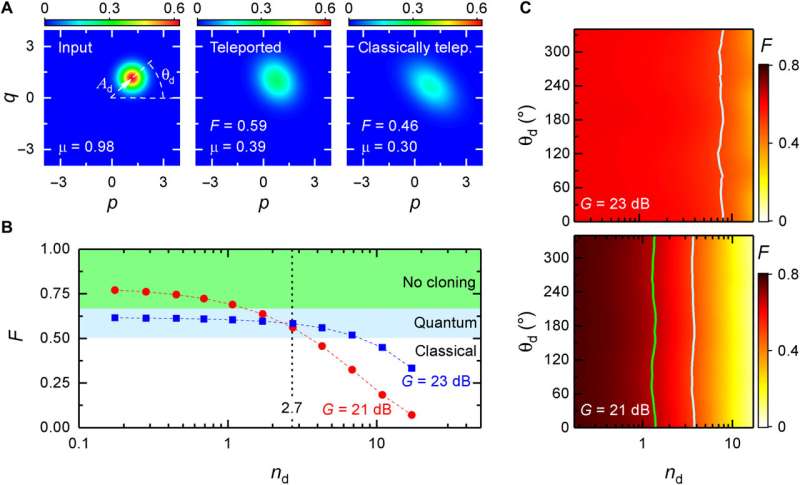
Experimental protocol and setup
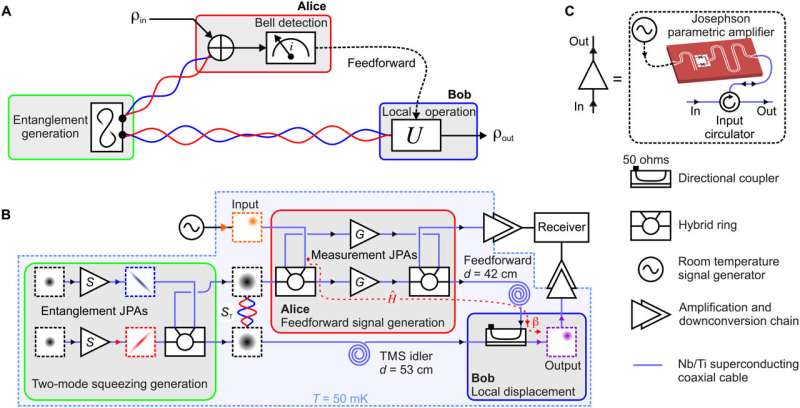
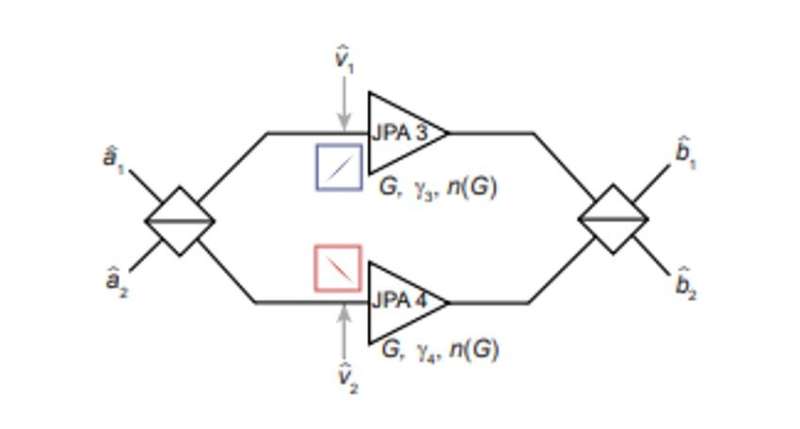
The experimental protocol of quantum teleportation contained several steps, including (1) entanglement generation and distribution between communication parties, usually named Alice and Bob. (2) Local operations on Alice's side aimed at generating a feedforward signal. (3) Feedforward and a local unitary operation on Bob's side, resulting in teleportation of the unknown quantum state by combining the feedforward signal with the entangled resource state. To accomplish this, Fedorov et al. used two entanglement Josephson parametric amplifiers (JPAs) in combination with a hybrid ring (microwave beam splitter) to generate path-entangled two-mode squeezed microwave states at the output of the hybrid ring. When superimposed at the hybrid ring, these states produced outputs that typically look like classical thermal noise. Due to the propagation of the two-mode squeezed states, they straightforwardly distributed the entangled states between Alice and Bob using superconducting niobium-titanium coaxial cables to implement step (1) of QT protocol, where the cables were shaped as half-wavelength waveguide resonators. On Alice's side, they used another hybrid ring to entangle a weak coherent state that served as the unknown input state with the shared two-mode squeezed state. The scientists guided the outputs of the second hybrid ring into a pair of measurement JPAs to perform strong phase-sensitive amplification along orthogonal amplification angles and superimposed the outputs of measurements at the third hybrid ring to produce the feedforward signal and conclude step (ii). During the final part of the QT protocol, the resulting feedforward application to Bob's part of the two-mode squeezed state implemented teleportation of the input state at the output of the directional coupler. This concluded step (iii) of the protocol.
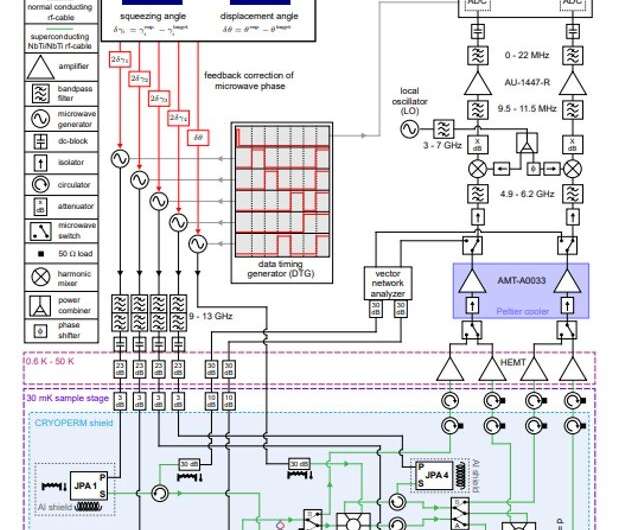
Quantum teleportation (QT) measurements
The experimental results of the microwave QT protocol showed the corresponding quantum-teleported output states and classically teleported output states. Fedorov et al. defined classical teleportation as the identical QT protocol without an entangled resource available to the communicating parties (Alice and Bob), implemented by switching off the pump tones of entanglement Josephson Parametric Amplifiers (JPAs), while the rest of the experimental protocol remained unaltered. However, the teleportation of a specific coherent state was not sufficient for general purposes of quantum communication. It is also important to demonstrate the successful teleportation of a set of quantum states to form a communication alphabet or codebook, where the orthogonality of quantum states forming the communication codebook are not required.
Outlook
In this way, Kirill G. Fedorov and colleagues succeeded to implement a quantum teleportation (QT) protocol with propagating microwaves in a cryogenic environment across a distance of 0.42 m. During the experiments, they relied exclusively on conventional aluminum-niobium superconducting parametric devices to generate and control quantum microwave signals that made them fully compatible with other quantum superconducting circuits, relative to frequencies and fabrication technology, including quantum memory cells or superconducting quantum processors. The QT results developed in the study combined with technical advances could bring quantum area networks between superconducting computers within reach. These experiments will pave the way in the convenient microwave regime toward superconducting quantum supercomputers to explore advantages of secure quantum communication.
More information: Kirill G. Fedorov et al, Experimental quantum teleportation of propagating microwaves, Science Advances (2021). DOI: 10.1126/sciadv.abk0891
Dik Bouwmeester et al, Experimental quantum teleportation, Nature (2002). DOI: 10.1038/37539
Journal information: Science Advances , Nature
© 2022 Science X Network