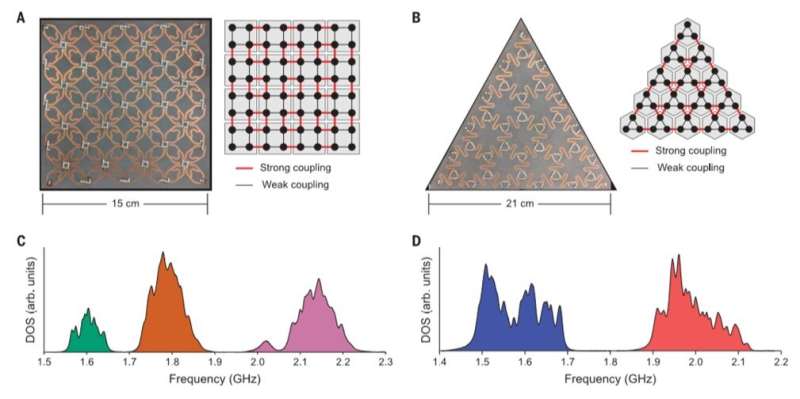
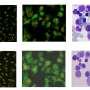
Fabricated metamaterials and measured spectra. (A) Photograph of the experimental resonator array with C4 symmetry. The schematic on the right illustrates the coupling between resonators. (B) Photograph of the experimental resonator array with C3 symmetry. The schematic on the right illustrates the coupling between resonators. (C) Measured DOS spectrum for the resonator array in (A). arb. units, arbitrary units. (D) Measured DOS spectrum for the resonator array in (B). Credit: Science, doi: science.sciencemag.org/content/368/6495/1114
Topological insulators (TIs) have an insulating interior and support conducting surface states with additional interfacing properties. The exotic metallic states on their surfaces can provide new routes to generate new phases and particles with potential applications in quantum computing and spintronics. Researchers have developed a theoretical framework to help identify and characterize such exotic states using new topological markers such as fractional charge density to detect topological states of matter. The resulting agreement between experimental work and theory has encouraged applications across topological platforms. In this work, Christopher W. Peterson and a team of scientists in electrical and computer engineering, physics, and mechanical science at the University of Illinois and the Pennsylvania State University in the U.S. discuss this new topological indicator introduced to identify higher-order topology and demonstrate the associated higher-order bulk-boundary correspondence. The work is now published on Science.
Topology is a branch of mathematics to study the properties of objects that are invariant (unchanged) when subject to smooth deformations. Topological insulators or materials with a gapped band structure (where no electronic states can exist) can be characterized by topological invariants i.e. a preserved property that cannot change as long as the material remains insulating, which can preserve the bulk bandgap and protective symmetries in materials. Additionally, the electronic band structure of a solid contains a range of energy levels with electrons. Ranges without electrons are known as bandgaps; the latter typically defines leftover ranges of energy that are not covered by any band. The mathematical field of topology is therefore a framework to study low-energy electronic structures of crystalline solids. Typically a bulk, insulating three-dimensional topological crystal contains a conducting two-dimensional surface state that facilitates topological bulk-boundary correspondence.
In this study, Peterson et al. focused on two-dimensional TIs. Materials with invariants protected by spatial symmetries are known as topological crystalline insulators (TCIs) and the team focused on a recently discovered class of TCIs classified as higher-order topological insulators (HOTIs). Thus far, scientists have only identified a few naturally occurring HOTIs by conducting many experimental studies in engineered metamaterials, including networks of coupled resonators, waveguide arrays and photonic or sonic crystals. They had also identified the nearest indicator of higher-order in such systems using spectroscopic measurements.
However, a fundamental problem exists with such spectral techniques since HOTIs can be mis-identified, even when their spectra do not exhibit in-gap modes. As a result, scientists aimed to establish an experimentally measurable indicator of higher-order topology protected by spatial symmetries. In this study, based on previous work, Peterson et al. demonstrated how a feature in metamaterials could be fractionally quantized to diagnose both first-order and higher-order topology in gapped TCIs (topological crystalline insulators). When investigating two-dimensions, the scientists named the quantity indicating second-order topology as a fractional corner anomaly (FCA). Second-order topological insulators or crystalline insulators contain gapped bulk and gapped crystalline boundaries with topologically protected gapless states at the intersection of the two boundaries. To observe the FCA experimentally, Peterson et al. constructed two rotationally symmetric TI metamaterials in microwave-frequency coupled resonator arrays.
They selected two insulators with different symmetries (square and triangle), since quantization of the fractional mode density and the FCA depended on the rotation symmetry of the group. The team demonstrated the first insulator on a square lattice with C4 symmetry and a second insulator on a kagome lattice with C3 symmetry (triangular shape). They identified the spectral density of states (DOS) of both metamaterials, using reflection measurements. The measured spectra of the C4-symmetric insulator showed three distinct bands, whereas the C3-symmmetric insulator showed two bands. Since neither insulator had in-gap modes it was difficult to determine if either metamaterial was topologically nontrivial based on the spectra alone.
Peterson et al. then calculated the mode density of the measured bands by including the local DOS (density of states) in each unit cell. The mode density of the C4-symmetric insulator had several important features, including the presence of bulk bands, symmetry-breaking disorder from fabrication imperfections and a non-zero fractional mode density in the edge and corner unit cells. They extracted the FCA (fractional corner anomaly) for each bulk band using the mode density data. Since a small amount of unavoidable disorder existed in the experiment with C4 symmetry, they averaged across all the edges to find the fractional mode density of the edge unit cell (σ) and averaged across all corners to find the fractional mode density of the corner unit cell (ρ). They similarly calculated the mode density for the C3-symmetric system. The nonzero FCA calculated in both metamaterials indicated that they were both HOTIs (higher-order topological insulators) with capacity to host second-order topological modes at their corners.
Peterson et al. noted the corner resonators around which the second-order topological modes were expected to exist, to be excited in band three of the C4-symmetric system. In the C3-symmetric system, the corner resonators were only excited in band two, indicating the energy of the corner modes to be too high. The scientists could spectrally localize the modes by slightly lowering the resonance frequency of corner resonators. The team applied a small negative potential to the corners to pull these modes into the bandgap. The experimental outcomes effectively captured the fundamental topological features protected by spatial symmetries; therefore, the scientists expect the results to help experimentally identify materials with higher-order topology. The new outcomes will simply help the experimental confirmation of new topological insulators.
More information: Christopher W. Peterson et al. A fractional corner anomaly reveals higher-order topology, Science (2020). DOI: 10.1126/science.aba7604
Frank Schindler et al. Higher-order topology in bismuth, Nature Physics (2018). DOI: 10.1038/s41567-018-0224-7
shraf El Hassan et al. Corner states of light in photonic waveguides, Nature Photonics (2019). DOI: 10.1038/s41566-019-0519-y
Journal information: Science , Nature Physics , Nature Photonics
© 2020 Science X Network