Pulse-driven robot: Motion via solitary waves

Scientists have recently explored the unique properties of nonlinear waves to facilitate a wide range of applications including impact mitigation, asymmetric transmission, switching and focusing. In a new study now published on Science Advances, Bolei Deng and a team of research scientists at Harvard, CNRS and the Wyss Institute for Biologically Inspired Engineering in the U.S. and France harnessed the propagation of nonlinear waves to make flexible structures crawl. They combined bioinspired experimental and theoretical methods to show how such pulse-driven locomotion could reach a maximum efficiency when the initiated pulses were solitons (solitary wave). The simple machine developed in the work could move across a wide range of surfaces and steer onward. The study expanded the variety of possible applications with nonlinear waves to offer a new platform for flexible machines.

Flexible structures that are capable of large deformation are attracting interest in bioengineering due to their intriguing static response and their ability to support elastic waves of large amplitude. By carefully controlling their geometry, the elastic energy landscape of highly deformable systems can be engineered to propagate a variety of nonlinear waves including vector solitons, transition waves and rarefaction pulses. The dynamic behavior of such structures demonstrate a very rich physics, while offering new opportunities to manipulate the propagation of mechanical signals. Such mechanisms can allow unidirectional propagation, wave guiding, mechanical logic and mitigation, among other applications.

In this work, Deng et al. were inspired by the biological retrograde peristaltic wave motion in earthworms and the ability of linear elastic waves to generate motion in ultrasonic motors. The team showed the propagation of nonlinear elastic waves in flexible structures to provide opportunities for locomotion. As proof of concept, they focused on a Slinky – and used it to create a pulse-driven robot capable of propelling itself. They built the simple machine by connecting the Slinky to a pneumatic actuator. The team used an electromagnet and a plate embedded between the loops to initiate nonlinear pulses to propagate along the device from the front to the back, allowing the pulse directionality to dictate the simple robot to move forward. The results indicated the efficiency of such pulse-driven locomotion to be optimal with solitons – large amplitude nonlinear pulses with a constant velocity and stable shape along propagation. The study expanded applications of solitary waves (solitons) while showing how they can be explored as simple underlying engines to assist flexible machines to move.

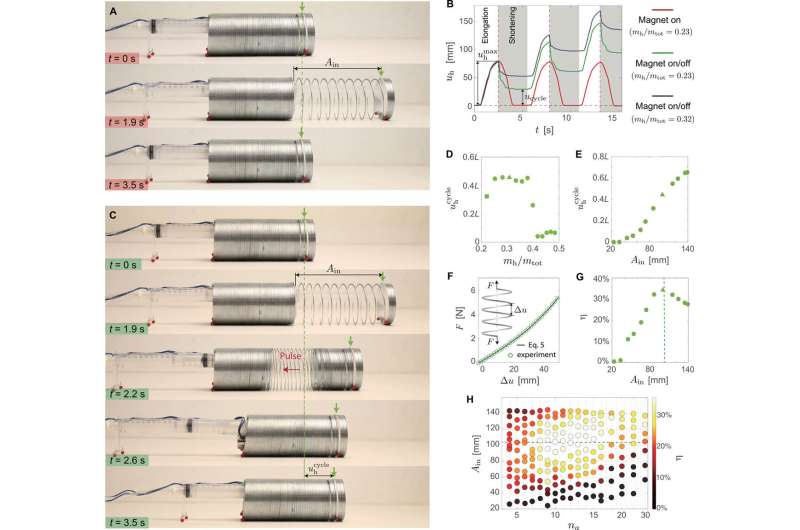
To create the Slinky robot, Deng et al. used a metal Slinky with a length of 50 mm and 90 loops, to then test and understand how to explore its intrinsic flexibility, and create a simple machine capable of movement. They connected two slinkies in series (100 mm, 180 loops) for a simple actuation strategy based on a pneumatic actuator, an electromagnet and three acrylic plates. They could stretch and shorten the setup using the pneumatic actuator while keeping the electromagnet on. The team tested the response of the machine by placing it on a smooth surface and monitoring it with a high-speed camera. Deng et al. then turned off the magnetic field in an attempt to break symmetry and cause the machine to crawl. They did not observe a reflected wave in the Slinky due to the large energy dissipation upon collision of the loops and instead observed clear forward movement of the robot. The team therefore explored the directionality introduced by the elastic waves to make the robot move—even in the presence of identical friction coefficients.

Attempts to make the flexible machine crawl via elastic pulses however revealed the experimental conditions to be suboptimal. For instance, they noticed backsliding immediately after turning off the electromagnet. To limit this motion, Deng et al. increased the mass at the head of the Slinky robot while optimizing the value to identify an optimal range. The Slinky maintained 10 loops between the front and loading plates in the setup. The team designated the maximum distance between the loading and front plates as A_in, which approximated 100 mm. To understand how the efficiency of the robot was a maximum for A_in = 100 mm Deng et al. carefully investigated the propagation of large-amplitude pulses through the Slinky.

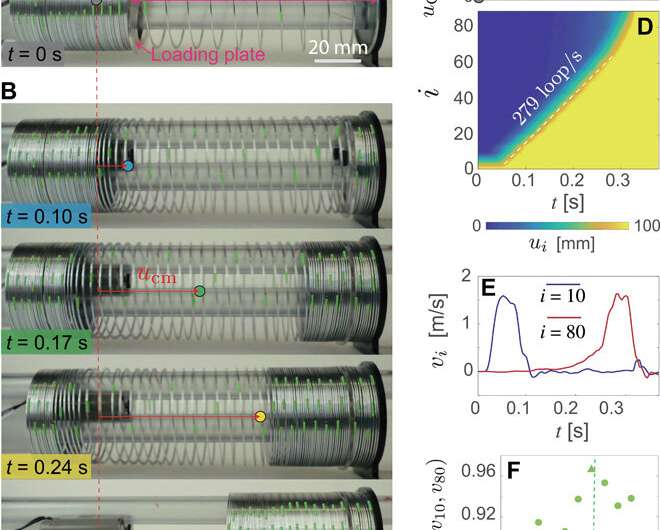
For these experiments, they focused on a single Slinky and monitored the position of green markers located at every other loop. They then initiated elastic waves that propagated towards the back by pre-stretching 10 loops near the front and turning off the electromagnet. The tests allowed the team to gather deeper insights to the propagation of pulses by monitoring the displacement of each loop. The scientists realized two main features of the robot; 1) the backward-propagating waves moved the center of mass of the Slinky forward and 2) the Slinky supported the propagation of large-amplitude solitary waves.

To gain further insight into the experimental results, Deng et al. developed a mathematical model that represented the mass and elasticity of an individual loop. The calculated results matched extremely well with the experimental outcomes and the model confirmed the experimental observations. The analysis further confirmed the efficiency of the Slinky robot to be at a maximum when the initiated waves were solitons. The nondispersive nature and compactness of solitary pulses made them extremely efficient to transfer the energy provided from the pneumatic actuator into motion in order to obtain the most efficient pulse-driven locomotion.

In this way, Deng et al. showed how backward propagating solitons could efficiently move a Slinky robot forward. Even though limbless organisms have previously bioinspired engineers to design a variety of robots, the team believe this work to be the first robotic system to rely on elastic pulses to move. The principles presented in the study were different from those used by ultrasonic motors, since the flexible Slinky robot used nonlinear pulse waves to change the position of the center of mass, ultrasonic motors are in contrast powered by linear sinusoidal waves. The team only focussed on rectilinear forward crawling in this work, but they can explore the flexibility of the Slinky to achieve a range of motions.

The team next intend to steer the robot by twisting the last loop at the back of the device and control the steering angle, while emphasizing the existing possibility to move the robot across a broad range of surfaces. Although Deng et al. only used a Slinky to realize pulse-driven locomotion in this work, the principles are general and can be expanded to a broad range of stretchable systems across scales to open avenues for microscale crawlers suited for medical applications.

© 2020 Science X Network