Computational origami: A universal method to wrap 3-D curved surfaces with nonstretchable materials

The counterintuitive question on how to wrap a curved spherical surface using conventionally stiff and non-stretchable or brittle materials, forms the basis of this study. To answer the question, Yu-Ki Lee and a research team in the departments of materials engineering and computer science in the Republic of Korea and the U.S. extended a geometrical design method of computational origami to wrap spherical constructs in a new report now published in Science Advances. The approach provided a robust and reliable method to engineer conformal devices for arbitrary curved surfaces using a computationally designed nonpolyhedral developable net. The computer-aided design transformed two-dimensional (2-D) materials such as silicon (Si) wafers and steel sheets into conformal structures that could fully wrap 3-D structures without fracture or deformation. The computational wrapping method allowed them to develop a design platform to transform conventionally non-stretchable 2-D devices into conformal 3-D curved surfaces.

The study introduced a universal method for conventional nonstretchable materials to wrap arbitrary and diverse 3-D curved surfaces by engineering conformal material devices without sacrificing their performance. For example, wrapping a sphere with a rectangular piece of paper can inevitably form wrinkles, while attempting to wrap a sphere with a tougher substrate can cause the wrapping material to fracture. To facilitate the process, materials scientists can introduce patterned cuts into the nonstretchable materials, including lattice cut patterns and fractal cut patterns to effectively wrap 3-D surfaces. Such concepts are shape programmable and can efficiently cover a sphere. Engineers have also recommended computer algorithms to design complex 3-D models based on 2-D auxetic structures. To achieve optimal coverage, they introduced a computational design strategy known as "computational wrapping with nonpolyhedral developable nets," to form nonstretchable material platforms for wearables and conformal devices.

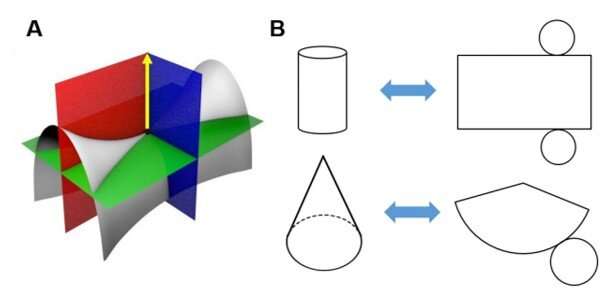
In theory, researchers can characterize a curved surface by the Gaussian curvature – which is the vector product of the maximum and minimum principal curvatures at a point. For example, a sheet of paper is called a 'developable surface' and represents a 2-D material with zero Gaussian curvature at all points. A developable surface cannot be transformed into a nondevelopable 3-D surface without tearing, stretching or compressing the material. The concept is mathematically proven by the "Gauss Theorema Egregium," which states that "To move a surface onto another surface the Gaussian curvature of all corresponding points must match." Computer scientists have exerted great efforts to algorithmically determine surface cuts that segment a nondevelopable surface into developable surface patches known as polyhedral nets or simply—nets. Recent computational methods aim to optimize net quality and foldability using machine learning methods in order to reduce the time and effort required for traditional trial and error approaches.

Since most real-world 3-D objects are smooth and curved, scientists require high-resolution meshes to cover the surfaces accurately. In this work, Lee et al. developed a new approach known as "computational wrapping" that goes beyond the conventional computational folding method. To accomplish this, they considered conformal device design as a paper wrapping problem instead of a paper folding (origami) challenge. The team recognized the functions of attaching and wrapping conformal devices to cover an underlying curved 3-D surface, simply by bending and pressing a polyhedral net without creases.

High resolution meshes allowed them to address the limits of long fabrication times and mechanical reliability. To enclose a surface with all-round non-zero Gaussian curvature, such as a perfect sphere, Lee et al. used a developable surface after refining the facet mesh to meet the required values of wrapping tightness. The results provided data on a nonpolyhedral developable net to create controlled and bound spaces between the net and sphere without gaps or overlaps between the facets. The fabrication process accurately produced highly complex and smooth 3-D surfaces many times faster than conventional computational folding methods when handling complex shapes using paper, metallic and ceramic wrapping materials. Finite element analysis supported that such computational wrappings were mechanically reliable.

The structures developed in the work led to a significant increase in computational origami for real-world industrial fabrication processes. For example, Lee et al. developed a conformal device using electroluminescent lamp (EL) panels to wrap a sphere, the resulting 3-D conformal device exhibited good function and they credited the results to bending and pressing processes used to wrap the sphere instead of creasing and folding techniques. The team also similarly demonstrated their method on a commercial Korean mask and on an electric toy vehicle with attached EL panels to function without failure. To generate the developable net for components with non-zero Gaussian surfaces such as the headlights of the electric toy vehicle, the scientists used the genetic algorithm (GA) unfolding method.

In this way, Yu-Ki Lee and colleagues introduced the concept of computational wrapping to convert nonstretchable 2-D flexible devices into 3-D conformal devices. Using the method, they enclosed a surface with non-zero Gaussian curvature such as a perfect sphere. The proposed technique could control the distance between the two surfaces to ensure tight wrapping. The work produced a single connected surface known as a nonpolyhedral developable net, designed to conformally wrap a 2-D sheet for any 3-D surface. As a result, the scientists were even able to facilitate stiff and brittle materials such as metal sheets and Si wafers to fully cover and wrap non-zero Gaussian curvature surfaces. The universal computational wrapping method developed in this work will provide new insights into the development of conformal devices with arbitrary shapes using efficient algorithms and robust, reliable fabrication methods.

© 2020 Science X Network