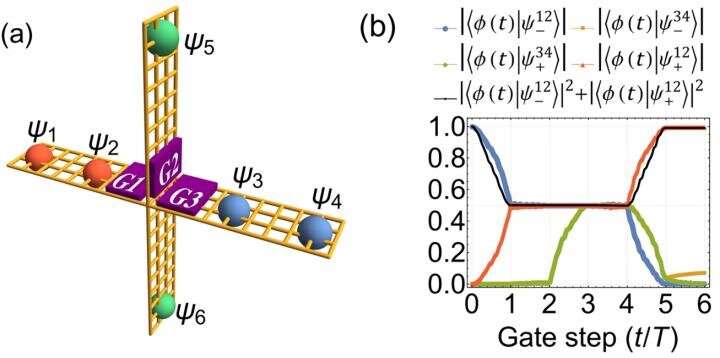
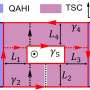
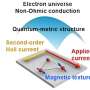
(a) Nanowire-based cross-shaped junction supporting the non-Abelian braiding of Jackiw-Rebbi zero-modes. (b) Numerical results for the evolution of wavefunction that demonstrates the non-Abelian braiding properties of Jackiw-Rebbi zero-modes. Credit: ©Science China Press
As an important branch of quantum computation, topological quantum computation has been drawing extensive attention for holding great advantages such as fault-tolerance. Topological quantum computation is based on the non-Abelian braiding of quantum states, where the non-Abelian braiding in the field of quantum statistics is highly related to the non-locality of the quantum states. The exploration on topological quantum computation in the last two decades is mainly focused on the Majorana fermion (or its zero-energy incarnation known as Majorana zero-mode), an exotic particle possessing non-Abelian statistics and well-known for its anti-particle being itself.
Jackiw-Rebbi zero-mode was firstly raised in the field of high energy physics in 1970s. With the growing importance of topology in the area of condensed matter physics, the concept of Jackiw-Rebbi zero-mode was also adopted to refer to the topologically protected zero-mode in the boundary of topological insulators. In contrast with the Majorana zero-mode only presented with a non-vanishing superconducting order parameter, Jackiw-Rebbi zero-mode is not self-conjugate and therefore could be presented even in the absence of particle-hole symmetry.
Recently, in a research article entitled as "Double-frequency Aharonov-Bohm effect and non-Abelian braiding properties of Jackiw-Rebbi zero-mode," published in National Science Review, researchers from four universities including Peking University and Xi'an Jiaotong University claimed a new method realizing non-Abelian braiding. Co-authors Yijia Wu, Haiwen Liu, Jie Liu, Hua Jiang, and X. C. Xie demonstrated that the Jackiw-Rebbi zero-modes widely existing in topological insulators also support non-Abelian braiding.
In this work, the authors constructed Jackiw-Rebbi zero-modes in a quantum spin Hall insulator. Through showing the Aharonov-Bohm oscillation frequency of the Jackiw-Rebbi zero-mode intermediated transport is doubled, they claimed that the Majorana zero-mode can be viewed as a special case of Jackiw-Rebbi zero-mode with particle-hole symmetry. In the method of numerical simulation, they also demonstrated that non-Abelian braiding properties are exhibited by Jackiw-Rebbi zero-modes in the absence of superconductivity. The authors believed that these results not only make theoretical progress exhibiting the charming properties of Jackiw-Rebbi zero-mode, but also provide the possibility realizing topological quantum computation in a non-Majorana (non-superconductivity) system.
This latest research also put forward a generalized and continuously tunable fusion rule in topological quantum computation when the degeneracy of Jackiw-Rebbi zero-modes is lifted. The authors concluded that Jackiw-Rebbi zero-mode could be a new candidate for topological quantum computation and holds additional advantages compared with its Majorana cousin: (1) the superconductivity is no longer required; (2) possesses generalized fusion rule; and (3) the energy gap is generally larger.
More information: Yijia Wu et al, Double-frequency Aharonov-Bohm effect and non-Abelian braiding properties of Jackiw-Rebbi zero-mode, National Science Review (2019). DOI: 10.1093/nsr/nwz189
Provided by Science China Press