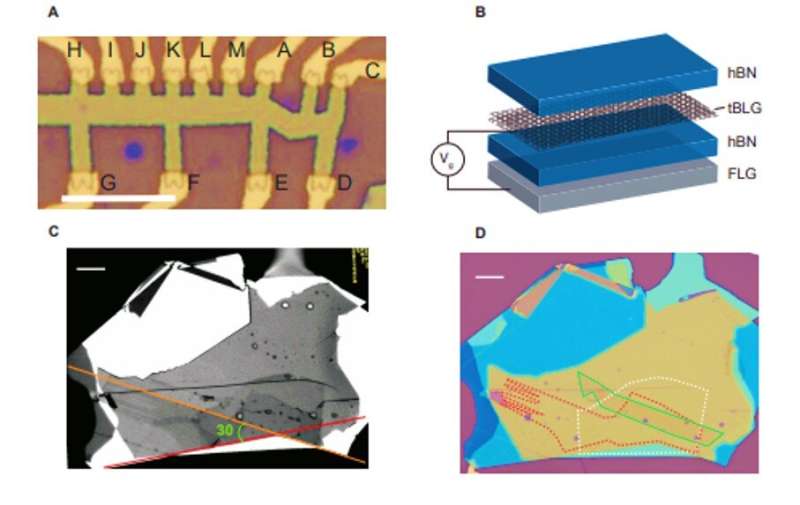
The tBLG device. (A) Optical micrograph of the device. Scale bar corresponds to 10 µm. (B) Schematic of a tBLG heterostructure. tBLG is encapsulated between flakes of hBN, with a flake of few-layer graphite used as a gate. (C) Optical image of the stack. The crystalline edge of the top hBN and the top layer of tBLG are aligned with a 30 degree angular offset in the marked cleavage planes. (D) Optical image of the stack before etching, showing the top layer of the tBLG (red dashed line), bottom layer of the tBLG (white dashed line), and the bottom gate (green solid line). Credit: Science, doi: 10.1126/science.aay5533
The quantum anomalous Hall (QAH) effect can combine topology and magnetism to produce precisely quantized Hall resistance at zero magnetic field (an environment carefully screened from magnetic fields). In a recent report on Science, M. Serlin and an interdisciplinary research team in the Department of Physics, National Institute of Materials Science and the Kavli Institute for Theoretical Physics in the U.S. and Japan detailed the observation of a QAH effect in twisted bilayer graphene aligned to hexagonal boron nitride. They drove the effect via intrinsic strong interactions, which polarized the electrons into a single spin and valley resolved moiré miniband (interference pattern).
When a magnetic field is applied at right angles to the current flow in a thin film, an electric field known as the Hall effect can be generated mutually perpendicular to the current and the magnetic field. An anomalous Hall effect requires combined magnetic polarization and spin-orbit coupling in the absence of an external magnetic field (hence the anomaly). When the anomalous Hall effect is quantized, it is known as the quantum anomalous Hall effect. In contrast to magnetically doped systems, the transport energy map measured by Serlin et al. was larger than the Curie temperature for magnetic ordering. Electrical currents as small as 1 nA could controllably switch the magnetic order between states of opposite polarization to form an electrically rewritable magnetic memory.
Physicists and materials scientists can classify two-dimensional insulators using the topology of their filled energy bands. In the absence of time reversal symmetry (conservation of entropy), nontrivial band topology can manifest experimentally as quantized Hall conductivity. Researchers are motivated by fundamental questions on the nature of topological phase transitions and their possible applications in resistance metrology and in topological quantum computing. They have devoted significant efforts to engineer quantized anomalous Hall effects with topologically protected quantized resistance in the absence of an applied magnetic field. Scientists had only thus far observed QAH effects in a narrow class of materials containing doped transition materials. The dopant magnetic moments in these materials broke time reversal symmetry, combined with the strongly spin-orbit coupled electronic structures to produce topologically nontrivial Chern bands (energy bands).
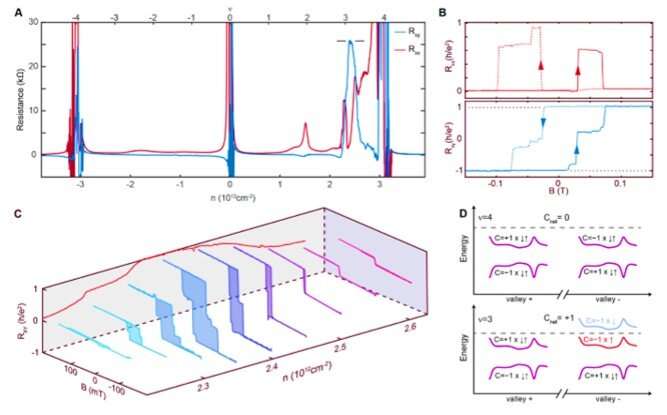
Quantized anomalous Hall effect in twisted bilayer graphene at 1.6 K. (A) Longitudinal resistance Rxx and Hall resistance Rxy as a function of carrier density n at 150 mT. Rxy reaches h/e2 and Rxx approaches zero near ν = 3. Data are corrected for mixing of Rxx and Rxy components by symmetrizing with respect to magnetic field at B = ±150 mT. (B) Longitudinal resistance Rxx and Hall resistance Rxy measured at n = 2.37 × 10^12 cm−2 as a function of B. Data are corrected for mixing using contact symmetrization. Sweep directions are indicated by arrows. (C) Hall resistance Rxy as a function of magnetic field B and density n. Hysteresis loop areas are shaded for clarity. The rear wall shows field-training symmetrized values of Rxy at B = 0. Rxy(0) becomes nonzero when ferromagnetism appears and reaches a plateau of h/e2 near a density of n = 2.37 × 10^12 cm−2. (D) Schematic band structure at full filling of a moiré unit cell (ν = 4) and ν = 3. The net Chern number Cnet ≠ 0 at ν = 3. Credit: Science, doi: 10.1126/science.aay5533.
The performance of these materials is, however, limited by the inhomogeneous distribution of magnetic dopants (additives), leading to structural, charge and magnetic disorder at the microscale. The resulting quantization therefore occurs at temperatures that are approximately an order of magnitude smaller than the magnetic ordering temperature. To engineer intrinsic quantum anomalous Hall effects, moiré graphene heterostructures provide two essential ingredients; topological bands and strong correlations. For instance, in hexagonal boron nitride (hBN) and twisted multilayer graphene, moiré patterns generically produce bands with finite Chern number, where time reversal symmetry of the single particle band structure can be enforced by canceling Chern numbers in opposite graphene valleys. For example, in specific heterostructures such as twisted bilayer graphene (tBLG) with an interlayer twist angle and rhombohedral graphene aligned to hBN, the bandwidth of Chern bands can be made exceptionally small. Scientists have demonstrated states of magnetic hysteresis (deviation from the theoretical value) relative to time-reversal symmetry breaking in tBLG and hBN heterostructures to show large anomalous Hall effects.
In the present work, Serlin et al. observed a QAH (quantum anomalous Hall) effect showing a robust magnetic field quantization in a flat band tBLG (twisted bilayer graphene) sample aligned to hBN (hexagonal boron nitride). They described the electronic structure of the flat-band tBLG via two distinct bands per spin and valley projection isolated from higher energy dispersive bands by an energy gap. The flat bands had a total capacity of eight electrons per unit cell, the research team defined the band filling factor as ν = nAm, where n equaled the electron density and Am equaled an area of 130 nm2 within the moiré unit cell.
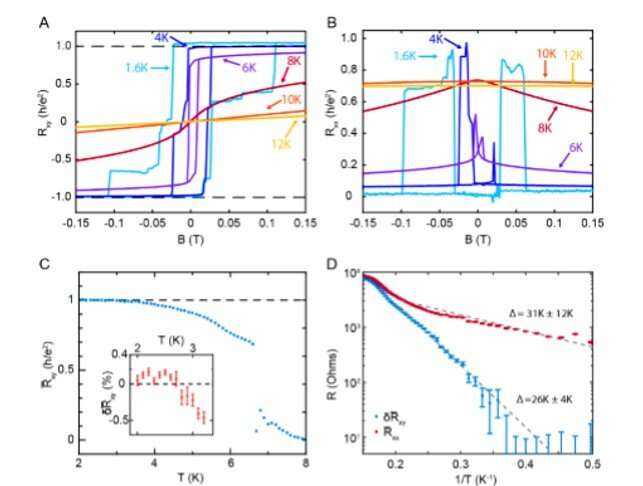
Temperature dependence of the quantum anomalous Hall effect. (A) Rxy and (B) Rxx as a function of B measured at various temperatures for n = 2.37 × 1012 cm−2. Rxx and Rxy mixing was corrected using contact symmetrization. (C) Temperature dependence of the field-training symmetrized resistance xy R at B = 0, as described in the main text. The Curie temperature was determined to be TC ≈ 7.5(.5) K using an Arrott plot analysis. Inset: detailed low temperature dependence of the deviation of xy R from the quantized value at B = 0. Error bars are the standard error derived from 11 consecutive measurements. xy R saturates below ≈3 K to a value determined by averaging the points between 2 and 2.7 K. (D) Arrhenius plots of field training symmetrized resistances at B = 0. Dotted lines denote representative activation fits. Systematic treatment of uncertainty arising from the absence of a single activated regime gives Δ = 31 ± 11 K and 26 ± 4 K. Credit: Science, doi: 10.1126/science.aay5533
The team recorded the longitudinal and Hall resistance at a magnetic field (B) of 150 mT and temperature (T) of 1.6 K, as a function of charge density across the entire flat band. They observed the Hall resistivity to be hysteretic (lagging in response to changing conditions) and the results showed a QAH state stabilized by spontaneously broken time reversal symmetry. The scientists only observed the quantized response for a particular choice of contacts at a specific compartment of the device. The observed magnetism arose from the 2-D nature of the graphene bands. Serlin et al. technically aligned the device to one of the hBN layers and based on the observations, predicted the hBN aligned samples to constitute a different class of tBLG devices with distinct phenomenology.
As the temperature of the system increased, the scientists observed a departure from resistance quantization and suppression of hysteresis with the Hall effect to demonstrate linear behavior in the field at 12 K. They observed finite hysteresis up to temperatures of 8 K, consistent with the Curie temperature (TC = 7.5 K). Thereafter, to quantitatively assess the energy scales associated with the QAH states, the team measured the activation energy at a lower temperature. They noted the activation energy to be several times larger than TC, in contrast to magnetically doped insulator films where the activations gaps were typically 10 to 50 times smaller than TC.
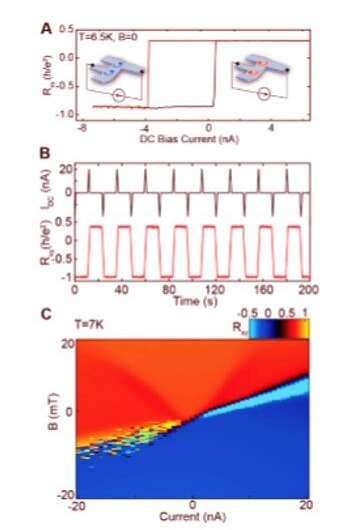
Current controlled magnetic switching. (A) Rxy as a function of applied DC current, showing hysteresis as a function of DC current analogous to the response to an applied magnetic field at 6.5 K. Insets: schematic illustrations of current controlled orbital magnetism. (B) Nonvolatile electrical writing and reading of a magnetic bit at T = 6.5 K and B = 0. A succession of 20 nA current pulses of alternating signs controllably reverses the magnetization, which is read out using the Hall resistance. The magnetization state of the bit is stable for at least 103 s (29). (C) Rxy as a function of both DC bias current and magnetic field at 7 K. Opposite directions of DC current preferentially stabilize opposite magnetization states of the bit. Measurements presented in (A to C) are neither field nor Onsager symmetrized, which why there is an offset in Rxy. Credit: Science, doi: 10.1126/science.aay5533
Since the ferromagnetic domains in tBLG can strongly interact with applied current to allow deterministic control within the device for domain polarization with exceptionally small DC currents. In the present work, the applied DC currents drove switching similar to that observed in an applied magnetic field, to produce hysteretic switching between magnetization states. Serlin et al. also obtained deterministic non-volatile electrical writing and reading of a magnetic bit using a succession of 20 nA current pulses to controllably reverse the magnetization, followed by a read-out using the large resulting change in the Hall resistance. The absolute magnitude of the current required to switch the magnetization state of the system approximated 10-9 A, considerably smaller than that reported in any previous system.
Based on the results, the team proposed a simple mechanism to explain the observed low-current switching that arose from the interplay of edge state physics and device asymmetry. Accordingly, in a QAH (quantum anomalous Hall) system, an applied current can generate a chemical potential difference between the chiral one-dimensional modes located on opposite sample edges. When the edges have different lengths or velocities, the current favored one of the two domains where the sign and magnitude of the effect was determined according to the device symmetry. In this way, M. Serlin and colleagues noted the observed effect to be generic to all QAH systems and likely to be dominant at low currents in tBLG due to weak pinning of magnetic domains and small device dimensions. The work provides an engineering parameter for electrical control of domain structure, which can be encoded deterministically into the device geometry.
More information: M. Serlin et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure, Science (2019). DOI: 10.1126/science.aay5533
Cui-Zu Chang et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator, Nature Materials (2015). DOI: 10.1038/nmat4204
Yuan Cao et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices, Nature (2018). DOI: 10.1038/nature26154
Journal information: Science , Nature Materials , Nature
© 2020 Science X Network