September 10, 2019 feature
Introducing quantum convolutional neural networks
Machine learning techniques have so far proved to be very promising for the analysis of data in several fields, with many potential applications. However, researchers have found that applying these methods to quantum physics problems is far more challenging due to the exponential complexity of many-body systems.
Quantum many-body systems are essentially microscopic structures made up of several interacting particles. While quantum physics studies have focused on the collective behavior of these systems, using machine learning in these investigations has proven to be very difficult.
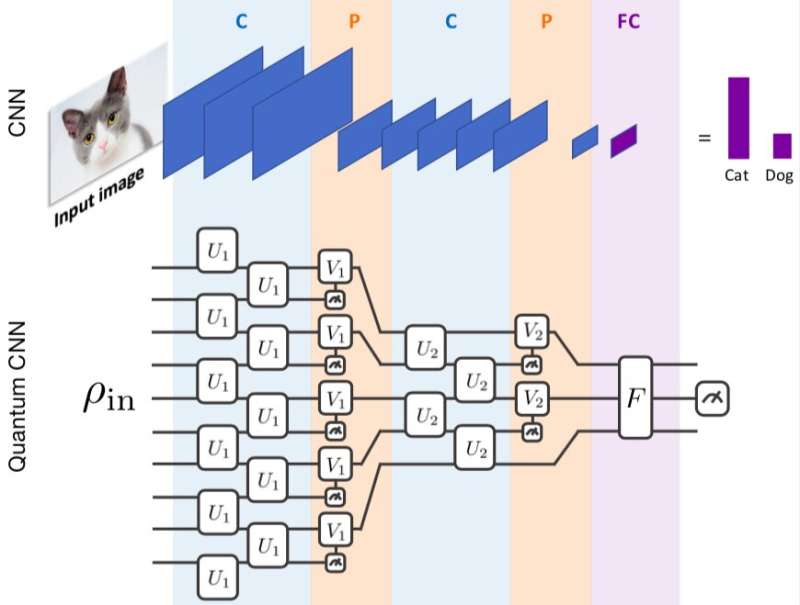
With this in mind, a team of researchers at Harvard University recently developed a quantum circuit-based algorithm inspired by convolutional neural networks (CNNs), a popular machine learning technique that has achieved remarkable results in a variety of fields. In their paper, published in Nature Physics, the researchers outlined this new architecture and evaluated its accuracy in recognizing quantum states associated with a 1-D, symmetry-protected topological phase.
"Our work is largely motivated by recent experimental progress to build quantum computers and the development of artificial intelligence based on neural network methods," Soonwon Choi, one of the researchers who carried out the study, told Phys.org. "In some sense, the idea to combine machine learning techniques and quantum computers/simulators is very natural: In both fields, we are trying to extract meaningful information from a large amount of complex data."
As a theoretical physicist investigating quantum many-body systems, Choi had often wondered whether there might be a more efficient way of analyzing the large amount of complex data obtained using quantum simulators. Artificial neural networks soon caught his attention, as they led to noteworthy results in several other tasks.
Transforming traditional machine learning approaches so that they could be effectively applied in quantum physics, however, appeared to be challenging. The main reason for this is that existing quantum simulators are quite small, thus they are unable to support a large-scale CNNs and other machine learning techniques that are being used in conventional computers.
"We had to make sure that all important features of conventional machine learning techniques are kept while our new algorithm is as compact as possible," Choi explained. "One of the objectives of the present work was to generalize a specific, well-known machine learning architecture called convolutional neural network (CNN) for a compact quantum circuit, and demonstrate its capabilities with simplistic but meaningful examples."
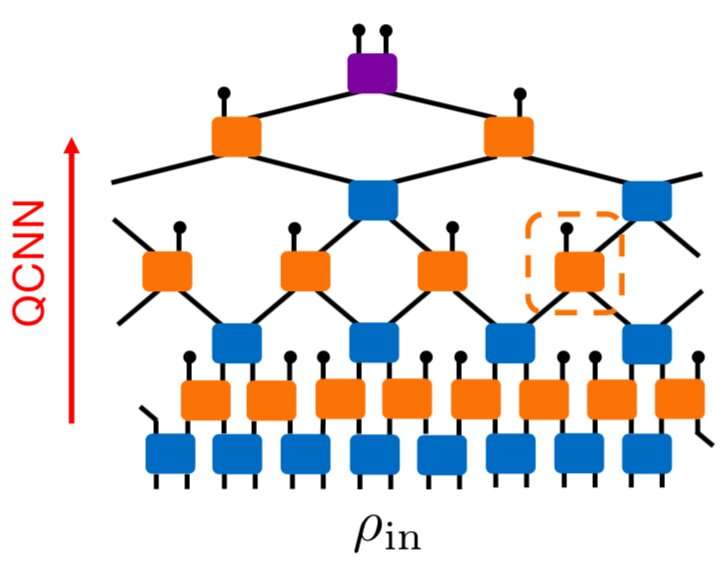
In their study, Choi and his colleagues assumed that CNNs owe their great success to two important features. Firstly, the fact that they are made out of smaller local units (i.e., multiple layers of quasi-local quantum gates). Secondly, their ability to process input data in a hierarchical fashion. The researchers found a connection between these two characteristics and two renowned physics concepts known as locality and renormalization.
"Locality is natural in physics because we believe that the law of nature is fundamentally local," Choi said. "Renormalization, on the other hand, is a very interesting concept. In physics, certain universal features of a quantum many-body system, such as the phase (e.g., liquid, gas, solid, etc.) of materials do not depend on (or are not sensitive to) microscopically detailed information of the system, but rather governed by only a few important hidden parameters. Renormalization is a theory technique to identify those important parameters starting from microscopic description of a quantum system."
The researchers observed that renormalization processes share some similarities with pattern recognition applications, particularly those in which machine learning is used to identify objects in pictures. For instance, when a CNN trained for pattern recognition tasks analyzes pictures of animals, it focuses on a universal feature (i.e., trying to identify what animal is portrayed in the image), regardless of whether individual animals of the same type (e.g., cats) look slightly different.
This process is somewhat similar to renormalization techniques in theoretical physics, which can also help to distill universal information. In their study, Choi and his colleagues tried to develop an architecture with the same key qualities as CNNs, but that would also be applicable to quantum physics problems.
"The resultant quantum circuit involves only log(n) number of parameters to be optimized for n-qubit input data, which is double exponential improvement compared to a naive approach, in which exp(n) number of parameters are optimized," Choi explained. "When the number of parameters to optimize becomes this small, one may worry that our circuit is not capable of complex information processing tasks. However, we have demonstrated that despite its small size, our quantum CNN is still capable of recognizing different quantum phases and designing quantum error correction schemes."
The researchers evaluated the technique they developed, called quantum convolutional neural network (QCNN), on a quantum physics-specific problem that involved recognizing quantum states associated with a 1-D symmetry protected topological phase. Remarkably, their technique was able to recognize these quantum states, outperforming existing approaches. As it is fairly compact, the QCNN could also potentially be implemented in small quantum computers.
"In my view, the most meaningful finding in our work is the connection between well-known physics concepts, renormalization (or more precisely, multiscale entanglement renormalization ansatz), and a successful information processing technique in artificial intelligence, CNN," Choi said. "Similar connections have been already suggested several years back, but here we have successfully substantiated the connection by explicitly demonstrating it with a clean example."
Choi and his colleagues are among the first to successfully create a CNN-inspired architecture that incorporates quantum physics. The examples outlined in their paper are also simple enough to be experimentally applied to existing and forthcoming quantum devices. Their results suggest that renormalization could be a promising quantum information processing technique and they thus intend to explore this idea further.
"We have demonstrated that our method allows to design quantum error correction schemes tailored for a given experimental system," Choi said. "It would be very exciting to see its action in exiting quantum computing platforms and improve their performance."
In their future work, Choi and his colleagues will first try to use their findings to develop new quantum computers. In addition, they would like to carry out further research investigating the relationship between CNNs or other neural network based methods and renormalization techniques.
"While we have demonstrated a nice example for one-dimensional quantum systems, more in-depth study of the connection in its full generality is still missing," Choi added. "In particular, studying the connection in two-dimensional quantum systems would be an exciting future direction."
More information: Iris Cong et al. Quantum convolutional neural networks, Nature Physics (2019). DOI: 10.1038/s41567-019-0648-8
Journal information: Nature Physics
© 2019 Science X Network