May 29, 2019 feature
On-demand, photonic entanglement synthesizer
Quantum information protocols are based on a variety of entanglement modes such as Einstein-Podolsky-Rosen (EPR), Greenberger-Horne-Zeilinger (GHZ) and other cluster states. For on-demand preparation, these states can be realized with squeezed light sources in optics, but such experiments lack versatility as they require a variety of optical circuits to individually realize diverse states of entanglement. In a recent study, Shuntaro Takeda and colleagues at the interdisciplinary departments of Applied Physics and Engineering in Japan addressed the shortcoming by developing an on-demand entanglement synthesizer. Using the experimental setup, the physicists programmably generated entangled states from a single squeezed source of light.
In the work, they used a loop-based circuit dynamically controlled at nanosecond time scales to process optical pulses in the time domain. The scientists generated and verified five different small-scale entangled states and a large-cluster containing more than 1000 modes in a single setup without changing the optical circuit. The circuit developed by Takeda et al. could store and release one part of the generated entangled states to function as a quantum memory. The experimental report published on Science Advances, will open a new way to build general entanglement synthesizers on-demand using a scalable quantum processor.
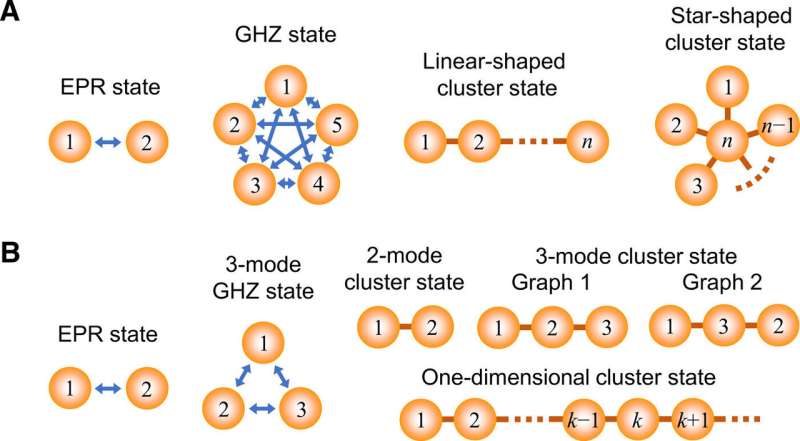
Entanglement is essential for many quantum information protocols in qubit and continuous variable (CV) regions, where they perform a variety of applications. For instance, the two-mode Einstein-Podolsky-Rosen (EPR) state is the most commonly used, maximally entangled state as a building block for two-party quantum communication and for quantum logic gates based on quantum teleportation. The generalized version of this state is an n-mode Greenberger-Horne-Zeilinger (GHZ) state central to building a quantum network, where the GHZ quantum state can be shared between n participants. For example, the n participants can communicate with each other for quantum secret sharing. For quantum computation on the other hand, a special type of entanglement known as cluster states has attracted much attention as a universal resource to allow one-way quantum computation.
The most convenient and well-established method in use at present to deterministically prepare photonic entangled states involves mixing squeezed light using beam splitter networks to generate entanglement in the continuous variable (CV) regime. Physicists have recently demonstrated large-scale entangled states by squeezing light sources multiplexed in the time domain or frequency domain. The method was not versatile since they had to design a variety of optical setups to produce the specific state of entanglement. Physicists had previously reported the programmable characterization of several types of entanglement in multimode quantum states using post-processing measurements or by changing the basis of measurement. The direct synthesis of a variety of entanglement states in a programmable, deterministic manner within a single framework remains a challenging task at present, therefore.
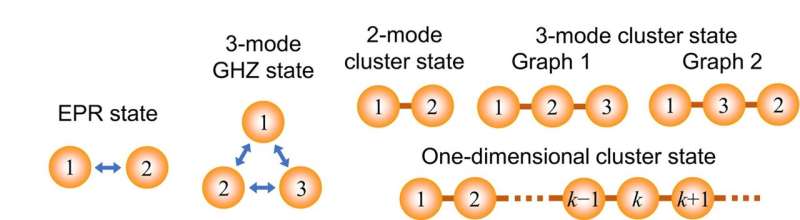
In the present work, Takeda et al. proposed an on-demand photonic synthesizer to programmably produce an important set of entangled states to resolve the existing challenge by including –
- An EPR state
- An n-mode GHZ state, and
- An n-mode linear or star-shaped cluster state for n≥2, in a single setup.
They based the synthesizer on a dynamic, controllable photonic circuit that processed optical pulses in the time domain. Using the circuit, the scientists verified the programmable generation of a variety of entangled states. The setup could also store and release one part of the generated entangled state to work as a quantum memory. The new method offers a promising route to photonic quantum information processability, which includes scalability and programmability.
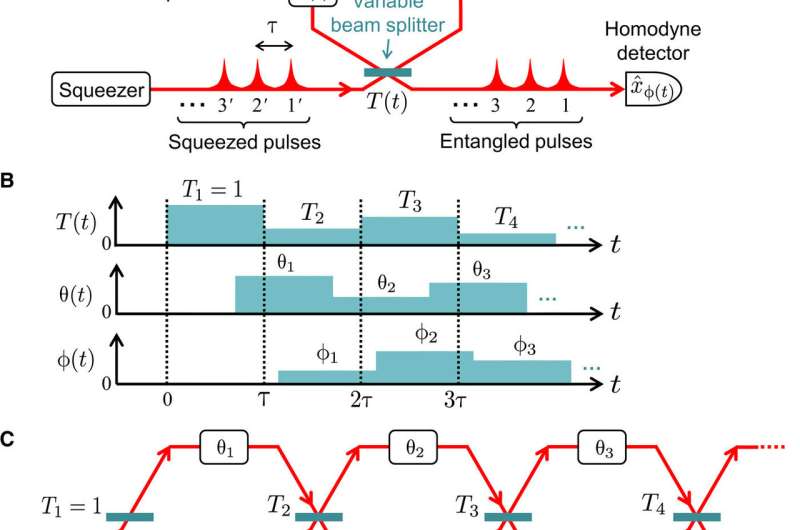
When forming the concept of an entanglement synthesizer, the scientists used a single squeezer to sequentially produce squeezed optical pulses in the study. They injected the pulses into a loop circuit whose round-trip time (τ) was equivalent to the time interval between the pulses. This loop included a beam splitter with variable transmissivity T (t) and a phase shifter with variable phase shift θ (t) – where t denotes time. After transmitting through the loop, the scientists directed the pulses to a homodyne detector using a tunable measurement basis. The circuit could synthesize a variety of entangled states from the squeezed pulses—for subsequent analysis.
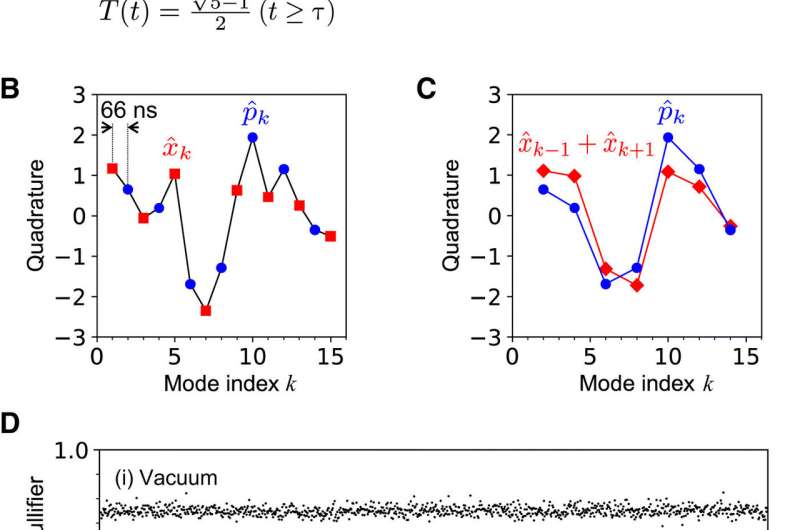
To demonstrate the generation of programmable entanglement, the scientists first programmed the synthesizer to generate five different small-scale entangled states. These included an (1) EPR state, (2) a three-mode GHZ, (3) a two-mode cluster state, and (4) a pair of three-mode cluster states. To verify the state of entanglement, the scientists applied temporal mode functions to the homodyne signal (wave function converted to an electrical signal) and extracted the quadrature of the broadband optical pulses to assess the correlation between different pulses.
They quantified the strength of correlation using inseparability parameters that were directly linked to the level of effective squeezing. The scientists were able to obtain results where the values satisfied the inseparability criteria derived in the study, to demonstrate the programmable generation of five different entangled states. They explained the values using the accumulated loss during squeezed light generation, entangled synthesis in the loop and during measurements.
Nevertheless, the experimental setup was unable to synthesize more than three-mode GHZ and cluster states due to design limitations of the electro-optic (EOM) modulator that drove the circuits. As a result, the scientists aim to develop a more sophisticated driving circuit or build cascading multiple EOMs to increase the number of selectable transmittivity values and generate a variety of GHZ and cluster states next.
The entanglement synthesizer could also produce large-scale entangled states for high scalability; shown with a one-dimensional cluster state. The circuit developed by the scientists was equivalent to the cluster state generation proposed previously and demonstrated by Yokoyama et al thereafter. In the present work, the scientists generated a one-dimensional cluster state for more than 1000 modes of entanglement. Due to technical limitations, the scientists could only measure 1008 modes in the experiment. However, in principle, this method does not have a theoretical limit for the number of entangled modes that can be generated.
The scientists were unable to directly compare the quality of these cluster states compared to the previous scheme by Yokoyama et al. as the present loop-based scheme was susceptible to losses due to additional optical components in the experimental setup. The component-based loss in the loop included a variable beam splitter and phase shifter, which led to loss accumulation when the optical pulses repeatedly circulated the setup.
Takeda et al. also formed a quantum memory by confining an optical pulse in the programmable loop circuit. Although the ability to add tunable delay to nonclassical CV states could play a key role for time synchronization in a variety of quantum protocols, physicists had only conducted a few quantum memory experiments for entangled continuous-variable (CV) states so far.
![Storage of one part of an EPR state in the loop. (A) Control sequence. (B) Measured inseparability parameter 〈[Δ(x̂1−x̂2)]2〉+〈[Δ(p̂1+p̂2)]2〉 with SE is plotted for each delay nτ (τ = 66 ns, n = 1, 2, …, 11). The yellow shaded area represents the inseparable region. Credit: Science Advances, doi: 10.1126/sciadv.aaw4530 On-demand, photonic entanglement synthesizer](https://scx1.b-cdn.net/csz/news/800a/2019/4-ondemandphot.jpg)
While a loop-based quantum memory is a simple and versatile memory that does not limit the wavelength or quantum state of light, it was only previously shown for single photons. Takeda et al. demonstrated the functionality in the present work by generating an EPR state in the loop and storing a part of the EPR state for n loops to then finally release it. The scientists could increase the lifetime of the quantum memory in the setup by increasing the mechanical stability of the loop or the feedback system to stabilize the quantum state. They were able to store any CV quantum state in the loop-based memory and also include non-Gaussian states by changing the squeezer to other quantum light sources.
In this way, Takeda et al. programmably generated and verified small-scale and large-scale entangled states and dynamically controlled the transmissivity of the beam splitter, phase shift and measurement basis of a loop-based optical circuit at nanosecond time-scales. They demonstrated the quantum memory capacity of the circuit by storing part of an EPR state in the loop. The system is programmable and highly scalable, offering a unique and versatile tool for future photonic quantum technologies.
Takeda et al. envision embedding this loop circuit in a larger loop to realize a nested arbitrary beam splitter network that combines the input squeezed pulses to synthesize arbitrary cluster states. They also foresee extensions of this circuit to a universal quantum computer by including a programmable displacement operator based on the homodyne detector's signal and non-Gaussian light source. The new network will form a crucial foundation to realize these goals and stimulate additional theoretical and experimental research in photonic quantum information processing.
More information: Shuntaro Takeda et al. On-demand photonic entanglement synthesizer, Science Advances (2019). DOI: 10.1126/sciadv.aaw4530
A. Einstein et al. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review (2002). DOI: 10.1103/PhysRev.47.777
Daniel M. Greenberger et al. Bell's theorem without inequalities, American Journal of Physics (2005). DOI: 10.1119/1.16243
K. Jensen et al. Quantum memory for entangled continuous-variable states, Nature Physics (2010). DOI: 10.1038/nphys1819
Journal information: Science Advances , American Journal of Physics , Nature Physics
Provided by Science X Network
© 2019 Science X Network