The splendid generative potential of the Sierpinski triangle

One transistor can become an oscillator with a surprising richness of behavior. However, even more interesting effects emerge if the structure of connections is fractal and shows some imperfections. Could similar rules explain the diversity and complexity of human brain dynamics?

Intuition suggests that self-similarity appears only in systems as complex as neural networks in the brain, or in fascinating shapes of nature, for example, in fractal Romanesco broccoli buds. At the Institute of Nuclear Physics of the Polish Academy of Sciences (IFJ PAN) in Cracow, researchers made a discovery that in some ways challenges this belief. In close collaboration with colleagues from the University of Catania and the University of Trento in Italy, the researchers constructed an elementary electronic oscillator based on just one transistor. As it turns out, when it contains fractal arrangements of inductors and capacitors, these generate amazingly rich characteristics of the electrical signals.

Many natural objects are fractal in nature, the whole is reflecting the shape of its parts. This extraordinary feature, known as self-similarity, is a distinguishing property of mathematical fractals. Self-similarity is also found in the shapes of clouds, coastlines, in the structure of plants or even in living organisms. Fractal properties are visible in the arrangement of the bronchi in the lungs, blood vessels in the brain, and, at a smaller scale, in the layout of dendrites and in the connections between neurons in the brain.

Scientists from all disciplines have long been fascinated by fractals. But it is only recently that engineers have started taking an interest in them for practical applications. Folding fractals shape long lines into small areas for the miniaturisation of antennas, for example. It is possible to build fractal circuits quite simply, by connecting standard inductors and capacitors according to a fractal pattern. Regardless of their physical size, such circuits would always have a self-similar shape and interesting properties. But so far, nobody has examined how they could perform in an oscillator.

"In our latest research, we started off from an extremely simple circuit that we had discovered last year. It is really tiny, as it only includes one transistor, two inductors, one capacitor and one resistor. Nevertheless, depending on the geometry of the connections and parameters of the inductors and capacitors, the circuit exhibits various, sometimes very complex activities. We wondered what would happen if we replaced the inductors with smaller and smaller self-similar circuits," says Dr. Ludovico Minati (IFJ PAN), the main author of the paper in the renowned scientific journal Chaos.

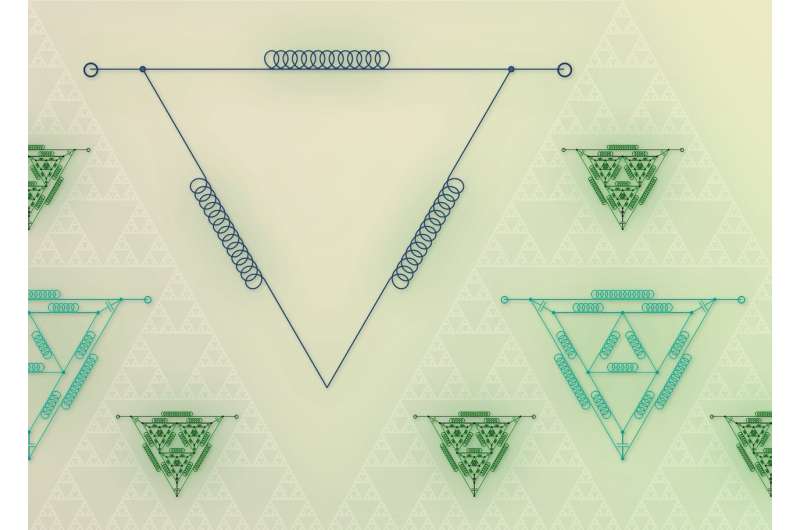
There are many patterns that can be repeated to generate fractals. One of the simplest starts by drawing a triangle, then taking the mid-points of its sides and connecting them. In this way, four smaller triangles are formed: three at the vertices and one in the middle. Then, the triangle in the middle is ignored, and the algorithm is iterated in the other triangles. A large number of these iterations leads to the formation of the Sierpinski triangle, from the name of a Polish mathematician who studied its remarkable properties. However, it has, in fact, been well known for centuries as a decorative element, and appears quite frequently in the floors of churches in the Lazio region of Italy, realised in the medieval period by the Marmorari Romani.

Intrigued by the idea of transforming the analyzed circuit into a fractal, the Cracow researchers attempted to recreate patterns of the Sierpinski triangle with inductors and capacitors. And here, they found a surprise. Although the circuits for laboratory tests were realized with the highest precision, the generated patterns failed to reach the same heights of complexity and aesthetic beauty observed in the simulations.

In simulations, the generated signals of a triangle of inductors are not complex. But inscribing more and more triangles, thereby increasing the depth of the fractal (meaning the number of nested levels, or iterations), makes the signals become increasingly intricate, delineating a motion in as many as 10 dimensions. However, in real circuits, such a level of dynamical richness is not reachable, and the number of dimensions decreases. It turns out that this is due to the fact that real components are not "ideal," effectively making the fractal more blurred.

"At first, we were quite disappointed. Later, we discovered something even more interesting than what we had initially planned to study. The key to remove the hindrance caused by the non-ideal elements was not to unblur the fractal structure, but to damage it," says Dr. Minati.

There is beauty in imperfection, according to artists, and the study of Cracow researchers seems to confirm this statement. By damaging the fractals slightly, for example, by removing some components or inserting some short circuits, it is possible to obtain much more complex resonances, which are readily confirmed by the experiment. These turned out to be similar to what would be obtained by reshuffling all components in a completely random manner. In a real, physically built circuit, these more complex resonances compensate for the non-ideal components, offering new ways of obtaining complex signals.

"Perfection belongs to mathematics, and neither to biology nor physics. Most of the fractals we observe in nature are not perfect at all, and we usually take this fact as an obvious flaw. Meanwhile, our understanding of the consequences of imperfections may be quite limited," says Prof. Stanislaw Drozdz (IFJ PAN, Cracow University of Technology).

The latest research shows that in simple, fractal electronic oscillators, imperfections in the structure of connections radically increase the dynamics of behavior. This result provokes some speculations related to the structure and functions of the human brain.

"We might be tempted to assume that imperfections in the layout of neural connections arise accidentally in a process of brain growth from a structure that would otherwise be ideal by definition. In fact, this is probably not the case, and their presence may serve a specific purpose and be a result of long-term natural selection. Neural networks with defects will manifest more complex dynamics. Who knows, then, if inspired by this observation, one day we will even intentionally build imperfect computers?" sums up Prof. Drozdz.