December 20, 2018 feature
Amoeba finds approximate solutions to NP-hard problem in linear time
Researchers have demonstrated that an amoeba—a single-celled organism consisting mostly of gelatinous protoplasm—has unique computing abilities that may one day offer a competitive alternative to the methods used by conventional computers.
The researchers, led by Masashi Aono at Keio University, assigned an amoeba to solve the Traveling Salesman Problem (TSP). The TSP is an optimization problem in which the goal is to find the shortest route between several cities, so that each city is visited exactly once, and the start and end points are the same.
The problem is NP-hard, meaning that as the number of cities increases, the time needed for a computer to solve it grows exponentially. The complexity is due to the large number of possible solutions. For example, for four cities, there are only three possible routes. But for eight cities, the number of possible routes increases to 2520.
In the new study, the researchers found that an amoeba can find reasonable (nearly optimal) solutions to the TSP in an amount of time that grows only linearly as the number of cities increases from four to eight. Although conventional computers can also find approximate solutions in linear time, the amoeba's approach is completely different than traditional algorithms. As the scientists explain, the amoeba explores the solution space by continuously redistributing the gel in its amorphous body at a constant rate, as well as by processing optical feedback in parallel instead of serially.
Although a conventional computer can still solve the TSP much faster than an amoeba, especially for small problem sizes, the new results are intriguing and may lead to the development of novel analogue computers that derive approximate solutions of computationally complex problems of much larger sizes in linear time.
How it works
The particular type of amoeba that the scientists used was a plasmodium or "true slime mold," which weighs about 12 mg and consumes oat flakes. This amoeba continually deforms its amorphous body by repeatedly supplying and withdrawing gel at a velocity of about 1 mm/second to create pseudopod-like appendages.
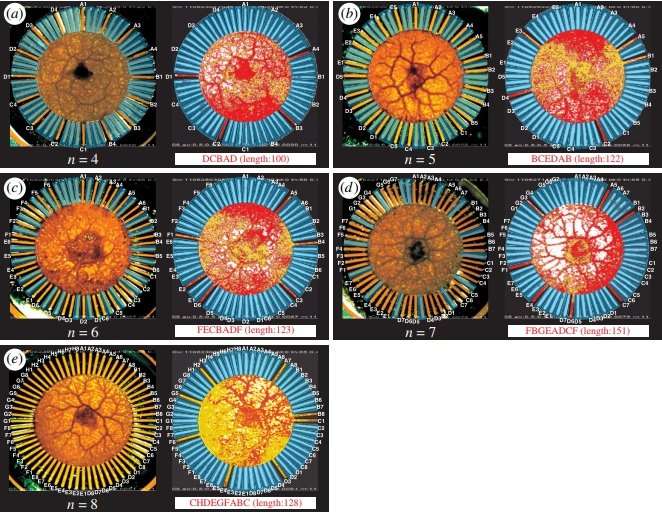
In their experiments, the researchers placed the amoeba in the center of a stellate chip, which is a round plate with 64 narrow channels projecting outwards, and then placed the chip on top of an agar plate. The amoeba is confined within the chip, but can still move into the 64 channels.
In order to maximize its nutrient absorption, the amoeba tries to expand inside the chip to come in contact with as much agar as possible. However, the amoeba does not like light. Since each channel can be selectively illuminated by light, it's possible to force the amoeba to retreat from the illuminated channels.
In order to model the TSP, each channel in the stellate chip represents an ordered city in the salesman's route. For example, in the case with four cities labeled A-D, if the amoeba occupies channels A4, B2, C1, and D3, then the corresponding solution to the TSP is C, B, D, A, C.
In order to guide the amoeba toward an optimal or nearly optimal solution, the key lies in controlling the light. To do this, the researchers use a neural network model in which every six seconds the system updates which channels are illuminated. The model incorporates information about the distance between each pair of cities, as well as feedback from the amoeba's current position in the channels.
The model ensures that the amoeba finds a valid solution to the TSP in a few ways. For example, once the amoeba has occupied a certain fraction of a particular channel, say A3, then channels A1, A2, and all other "A" channels are illuminated in order to prohibit city A from being visited twice. Also, B3, C3, D3, and all other "3" channels are illuminated to prohibit simultaneous visits to multiple cities.
The model accounts for the distances between cities by making it easier to illuminate channels that represent cities with longer distances than with shorter distances. For instance, say the amoeba occupies channel B2, and has begun to encroach into channels C3 and D3 in equal amounts, and the distance between cities B and C is 100 while the distance between cities B and D is 50. The longer distance between B and C eventually causes the system to illuminate channel C3, causing the amoeba to retreat from that channel but allowing it to continue moving into D3.
Overall, modeling the TSP with an amoeba harnesses the amoeba's natural tendency to seek out a stable equilibrium. As channels representing shorter routes are less likely to be illuminated, the amoeba may spread out in those channels and continue to explore other non-illuminated channels in order to maximize its surface area on the agar plate.
The researchers also developed a computer simulation called AmoebaTSP that mimics some of the main features of how the amoeba addresses the problem, including the continuous movement of gel as it is supplied at a constant rate and withdrawn from various channels.
"In our stellate chip for solving the n-city TSP, the total area of the body of the amoeba becomes n when the amoeba finally finds an approximate solution," Aono told Phys.org. "There seems to be a 'law' that the amoeba supplies its gelatinous resource to expand in the non-illuminated channels at a constant rate, say, x. This law would be kept even when some resources bounce back from illuminated channels. Then the time required to expand the body area n to represent the solution becomes n/x. This mechanism would be the origin of the linear time, and it was reproduced by our computer simulation model.
"But still, the mechanism by which how the amoeba maintains the quality of the approximate solution, that is, the short route length, remains a mystery. It seems that spatially and temporally correlated movements of the branched parts of the amoeba located at distant channels are the key. Each of these branches is oscillating its volume with some temporal 'memory' on illuminated experiences. Groups of the branches perform synchronization and desynchronization for sharing information even though they are spatially distant."
In the future, the researchers plan to further improve the amoeba's computing abilities.
"We will investigate further how these complex spatiotemporal oscillatory dynamics enhance the computational performance in finding higher-quality solutions in shorter time," said coauthor Song-Ju Kim at Keio University. "If it could be clarified, the knowledge will contribute to create novel analogue computers that exploit the spatiotemporal dynamics of electric current in its circuit.
"Of course, running some other algorithms on traditional digital computers for linear time, we can derive approximate solutions to TSP. On the other hand, when running our simulation models (AmoebaTSP or its developed versions) on the traditional computers as we did in this study, the analogue and parallel spatiotemporal dynamics require nonlinear time for simulating them as digital and serial processes. So we are trying to obtain much higher-quality solutions than those derived from the traditional ones by running our models on the analogue computers for linear time or shorter."
The researchers also expect that, by fabricating a larger chip, the amoeba will be able to solve TSP problems with hundreds of cities, although this would require tens of thousands of channels.
More information: Liping Zhu, Song-Ju Kim, Masahiko Hara, and Masashi Aono. "Remarkable problem-solving ability of unicellular amoeboid organism and its mechanism." Royal Society Open Science. royalsocietypublishing.org/doi/10.1098/rsos.180396
Journal information: Royal Society Open Science
© 2018 Science X Network