Correcting the eyesight of microscopes

Scientists have discovered a new property of wave propagation that leads to a new way to improve the resolution of virtually all optical technologies, including microscope lenses, telecommunications, laser-based lithography, biological and astronomical imaging. All these systems transmit information and energy through wave propagation. Researchers at the Institute for Basic Science have discovered that if light passes through asymmetric apertures, astigmatism arises and can degrade image resolution. Having identified this previously unsuspected problem, the researchers showed how to remedy it.

While reading, the eye lens focuses light to the back of the eye. However, if the lens's horizontal and vertical focusing power is different, this text will appear blurred: For example, the vertical and horizontal lines that form the letter "T" will not come into focus together. To avoid this focusing defect, artificial lenses are optimally designed to change the shape of the light wavefronts from planar into perfectly spherical wavefronts, because it is believed that spherical wavefronts necessarily focus at their unique center of curvature. Published in Proceedings of the National Academy of Sciences (PNAS), this study shows that scientists should re-examine this belief and revisit their design strategies.

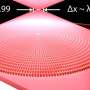
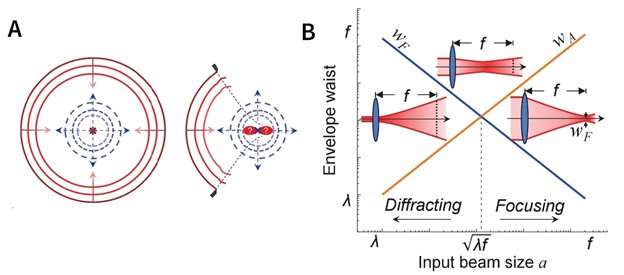
An example of wave propagation is circular waves created by a pebble dropped into a pond. The exact point where the pebble hits the water determines the position and the shape of the waves. If you could go back in time, those circular waves would refocus on the initial impact point precisely, because the information on the point location is not lost during wave propagation. This 2-D example can be extended to a 3-D situation in which waves are spherical and refocus exactly at the center of the sphere. However, in real life, light generally focuses from one side along some direction and not from all directions, and the ideal picture of focusing from a full circle or a full sphere is never exactly relevant.

"A full spherical wave is symmetric and has its focus exactly at the center of the sphere. However, to keep this spherical symmetry, light should propagate from all directions onto the sample. And this virtually never happens. Wavefronts are passed through an aperture that is limited to a portion of a sphere, instead of the full sphere. Consequently, spherical symmetry is broken and information is lost," says Prof. Francois Amblard, corresponding author of the study. In the case of the pond, this would be similar to going back in time to try to refocus a limited wave arc, instead of the full circular waves: These arc waves would not necessarily converge on the same impact point, because information about the center location is partially lost.

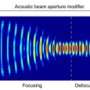
The IBS team has proved that as the aperture gets smaller, the focus shifts backward toward the lens, such that the initial focus is no longer in focus. As a consequence, if the aperture is not equal in the vertical and horizontal planes, focal shifts will differ between these directions, leading to astigmatism. "Astigmatism can occur even with the most perfect lens if it is used with a non-circular aperture," explains Kai Lou, first author of the study.

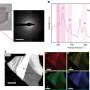
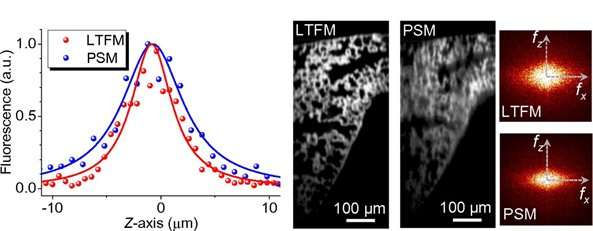
The team applied the idea to improve a technique called line-temporal focusing microscopy (LTFM, also called spatiotemporal focusing), which makes use of a naturally asymmetric input beam. As LTFM is a method used to visualize deep biological structures, the researchers tested their focal shift correction strategy with mouse lung tissues. An unprecedented resolution was obtained, that even outperformed a classical technique called point scanning microscopy (PSM).

How does this knowledge contribute to improved resolution? Even though this effect is very small and can be ignored for ordinary applications, correcting for aperture-induced astigmatism could make a significant difference in delicate systems like advanced microscopy. Understanding that astigmatism is intrinsic to the broken circular symmetry could help design corrections tailored to the aperture shape, especially in fields such as astronomy, telecommunication, or with ultrasounds, where non-circular apertures cannot be avoided.

"In the future, we plan to apply aperture-induced astigmatism to even more complex information transfer technologies," said Steve Granick, co-correspondent author of this study. "Moreover, the study opens avenues to basically improve the design of any equipment handling electromagnetic waves, ultrasounds, or particles beams. For example, it also applies to waves, used with space antennas to focus on satellite or spaceship. We believe it can contribute to design better systems in synthetic microscopic eyesight, telecommunications, and even microwave devices."