Bayesian model selection shows extremely polarized behavior when the models are wrong

Scientists from University College London (UCL) and the Academy of Mathematics and Systems Science, Chinese Academy of Sciences (CAS, AMSS), have reported progress in understanding problems associated with Bayesian model selection. The research suggests that the Bayesian method tends to produce very high-posterior probabilities for estimated evolutionary trees even if the trees are clearly wrong, and offers a possible explanation for this phenomenon.

Model comparison is widely used in various branches of sciences in which scientific hypotheses are formulated as statistical models and tested using observed data. However, model comparison is a thorny issue in both classical statistics and Bayesian statistics.

In classical statistics, two nested models are compared. The framework does not work when the compared models are not nested. In contrast, Bayesian statistics compares different models by calculating their posterior probabilities, which indicates our confidence or belief in the model.

Not only do the two methodologies spring from drastically different philosophies, they may also produce opposite conclusions in the analysis of the same data. Bayesian model selection is known to converge to the true model if the true model is included among the models under consideration.

That is, when scientists collect more data, the posterior probability for the right model will increase and approach 100 percent, and they will thus be increasingly certain which is the true model.

However, if all the considered models are wrong, the behavior of the Bayesian method is unknown.

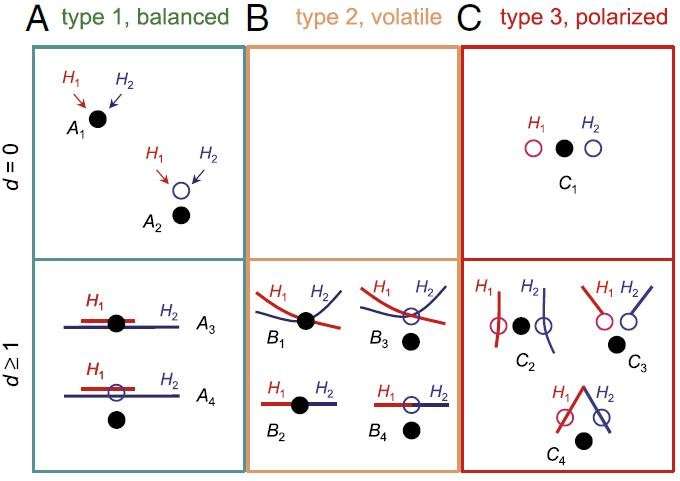
Scientists have characterized Bayesian model selection problems, and categorized them into three types, each of which shows a different behavior.

In the most scientifically interesting case, i.e., when the compared models are distinct and nearly equally wrong, Bayesian model selection shows problematic polarized behavior: It tends to support one model with full force in some datasets, but support another model in other datasets.

The result may be summarized using the following analogy: Suppose the world is gray, but we ask a sage whether it is black or white. He takes a deep look at the world and says it is black, with total confidence. But the next time we ask the same question, he says it is white, again with total confidence.

This study was motivated by problems in molecular phylogenetics, which is the science of working out the relationships among species using genetic data, represented by evolutionary trees.

These different trees are opposing statistical models in the Bayesian analysis of the data. Evolutionary biologists have long observed that the method tends to produce very high posterior probabilities for the estimated evolutionary trees (very often 100 percent), even if the trees are clearly wrong.

Our results provide a possible explanation for this unpleasant behavior. The implications of the results for the use of Bayesian model selection in testing opposing scientific hypotheses in general are yet to be explored.