Physicists create first direct images of the square of the wave function of a hydrogen molecule

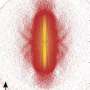
For the first time, physicists have developed a method to visually image the entanglement between electrons. As these correlations play a prominent role in determining a molecule's wave function—which describes the molecule's quantum state—the researchers then used the new method to produce the first images of the square of the two-electron wave function of a hydrogen (H₂) molecule.

Although numerous techniques already exist for imaging the individual electrons of atoms and molecules, this is the first method that can directly image the correlations between electrons and allow researchers to explore how the properties of electrons depend on one another.

The researchers, M. Waitz et al., from various institutes in Germany, Spain, the US, Russia, and Australia, have published a paper on the new imaging method in a recent issue of Nature Communications.

"There are other methods that allow one to reconstruct correlations from different observations; however, to my knowledge, this is the first time that one gets a direct image of correlations by just looking at a spectrum," coauthor Fernando Martín at the Universidad Autónoma de Madrid told Phys.org. "The recorded spectra are identical to the Fourier transforms of the different pieces of the square of the wave function (or equivalently, to the representation of the different pieces of the wave function in momentum space). No reconstruction or filtering or transformation is needed: the spectrum directly reflects pieces of the wave function in momentum space."

The new method involves combining two imaging methods that are already widely used: photoelectron imaging and the coincident detection of reaction fragments. The researchers simultaneously employed both methods by using the first method on one electron to project that electron onto a detector, and using the second method on the other electron to determine how its properties change in response.

The simultaneous use of both methods reveals how the two electrons are correlated and produces an image of the square of the H₂ correlated two-electron wave function. The physicists emphasize one important point: that these are images of the square of the wave function, and not the wave function itself.

"The wave function is not an observable in quantum physics, so it cannot be observed," Martín said. "Only the square of the wave function is an observable (if you have the tools to do it). This is one of the basic principles of quantum physics. Those who claim that they are able to observe the wave function are not using the proper language because this is not possible: what they do is to reconstruct it from some measured spectra by making some approximations. It can never be a direct observation."

The researchers expect that the new approach can be used to image molecules with more than two electrons as well, by detecting the reaction fragments of multiple electrons. The method could also lead to the ability to image correlations between the wave functions of multiple molecules.

"Obviously, the natural step to follow is to try a similar method in more complicated molecules," Martín said. "Most likely, the method will work for small molecules, but it is not clear if it will work in very complex molecules. Not because of limitations in the basic idea, but mainly because of experimental limitations, since coincidence experiments in complex molecules are much more difficult to analyze due to the many nuclear degrees of freedom."

The ability to visualize electron-electron correlations and the corresponding molecular wave functions has far-reaching implications for understanding the basic properties of matter. For instance, one of the most commonly used methods for approximating a wave function, called the Hartree-Fock method, does not account for electron-electron correlations and, as a result, often disagrees with observations.

In addition, electron-electron correlations lie at the heart of fascinating quantum effects, such as superconductivity (when electrical resistance drops to zero at very cold temperatures) and giant magnetoresistance (when electrical resistance greatly decreases due to the parallel alignment of the magnetization of nearby magnetic layers). Electron correlations also play a role in the simultaneous emission of two electrons from a molecule that has absorbed a single photon, a phenomenon called "single-photon double ionization."

And finally, the results may also lead to practical applications, such as the ability to realize correlation imaging with field-electron lasers and with laser-based X-ray sources.

© 2018 Phys.org