December 4, 2017 feature
Grasshopper problem yields insight into quantum theory
(Phys.org)—Like many mathematical puzzles, the grasshopper problem is simple to state but difficult to solve: A grasshopper lands at a random point on a lawn of area 1, then jumps once, a fixed distance, in a random direction. What shape should the lawn be in order to maximize the chance that the grasshopper stays on the lawn after jumping?
A first impression may be that the lawn should be in the shape of a circle, at least when the distance the grasshopper jumps is small. However, Olga Goulko and Adrian Kent, the two physicists who introduced the grasshopper problem in a new paper, have mathematically proved that a disc-shaped lawn is not optimal for any distance.
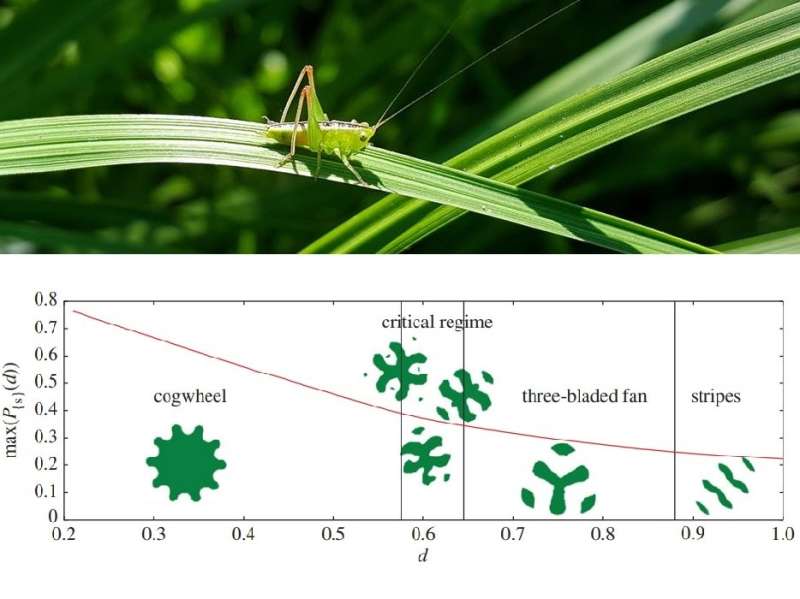
Instead, they discovered through numerical simulations that the optimal lawn shape takes on a variety of complex shapes for different jumping distances, such as a cogwheel shape for distances smaller than 1/π1/2 (the radius of a circle of area 1, or approximately 0.56), while for larger distances, the optimal lawn consists of disconnected pieces. Often, but not always, these optimal shapes possess some type of symmetry.
Motivated by physics
Aside from being an interesting geometry problem, the grasshopper problem is also closely related to research in quantum physics and may have a variety of technological applications. In particular, the grasshopper problem is connected to the Bell inequalities, which famously show that, unlike classical physics models, quantum theory does not obey local realism. A prime example of the violation of local realism is seen in quantum entanglement, in which two distant entangled systems exhibit correlations that cannot be explained by any model that obeys local realism.
This connection to the Bell inequalities is, in fact, what originally motivated Goulko and Kent to propose the grasshopper problem. An open problem in physics regarding the Bell inequalities is to determine the optimal bounds that are violated by quantum theory when quantum correlations are measured on a sphere at angles between 0 and 90 degrees. It turns out that this problem of determining the optimal bounds is equivalent to the problem of determining the lawn shape of the grasshopper problem when the lawn is spherical rather than flat ground. In the spherical version of the grasshopper problem, the distance the grasshopper jumps over flat ground is replaced by the angle at which it jumps across the sphere.
In their paper, which is published in a recent issue of the Proceedings of The Royal Society A, Goulko and Kent have only analyzed the planar version of the grasshopper problem, although they expect that it should not be too difficult to apply the same numerical techniques to the spherical case. Then, when accounting for some additional constraints, it may be possible to finally resolve the problem of optimal bounds of the Bell inequalities.
"We plan to move on to work on the spherical versions of the grasshopper problem relevant to Bell inequalities, and expect that our methods should work there," Kent told Phys.org.
New frontier
As the physicists explain, one of the surprising things about the grasshopper problem is that nothing quite like it has ever been proposed before. Although the basic idea is straightforward enough that the problem could have been posed by the ancient Greek mathematician Euclid, who laid the foundations of modern geometry, the researchers are not aware of any previous version of the problem, either in ancient or modern times.
"It is nice to be reminded that, even in a field as old as geometry, one can still find simple novel questions that have surprising answers and open up new lines of research," Kent said.
As a brand new problem, there are an endless number of future research directions to take. For instance, the physicists suggest allowing the grasshopper to take multiple jumps, or requiring that the grasshopper walk and remain on the lawn at all points of its path (a variation which they call the "ant problem"). Other possible variations include generalizing to higher dimensions, analyzing lawn surfaces other than spheres and planes, considering a variation of the problem with two different species of lawn seed that can overlap in the same region (which is particularly relevant for Bell inequalities), and placing additional restrictions on the possible solutions.
Of course, such questions are not really about grasshoppers and lawns, as the underlying structure offers a way to model various real-world situations. One example that the researchers point out is nuclear chain reactions. In a chain reaction, a high-energy particle impacts a random atomic nucleus, causing it to undergo fission, which produces another high-energy particle that travels a certain distance to hit another random nucleus, and the process repeats. By modeling this situation with the grasshopper problem, the optimal lawn area corresponds to the maximum initial reaction rate, which maximizes the number of nuclei that participate in the chain reaction.
Another potential application of the grasshopper problem lies in modeling quantum communication protocols, which the researchers explain can be thought of as a grasshopper model in which one party must choose which algorithm (lawn shape) to use to communicate with a second party.
And finally, the researchers suggest that it may be interesting to look into the origins of the lawn shapes themselves, as some of the lawn patterns resemble patterns that repeatedly emerge in nature, such as in flowers, seashells, and animal stripes. In accordance with the theory of morphogenesis proposed by Alan Turing, these patterns may arise as optimal solutions for chemical reasons, which may help explain the diverse and complex shapes of the lawns that appear in the grasshopper problem.
More information: Olga Goulko and Adrian Kent. "The grasshopper problem." Proceedings of The Royal Society A. DOI: 10.1098/rspa.2017.0494
Journal information: Proceedings of the Royal Society A
© 2017 Phys.org