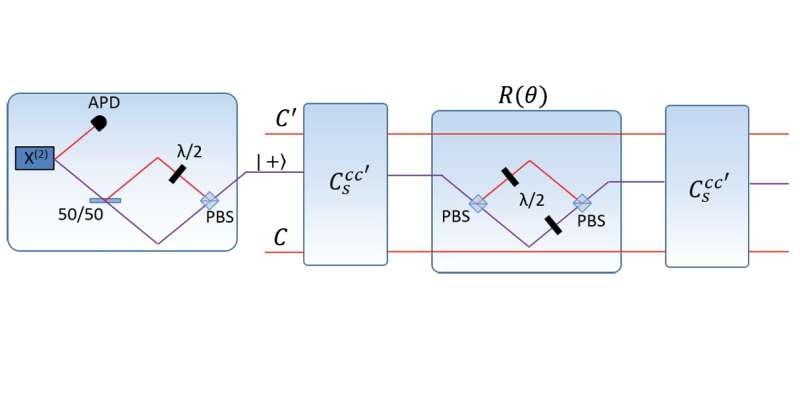
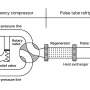
The proposed optical set-up that could be used to implement the new quantum machine learning algorithm over infinite dimensions. Credit: Lau et al. ©2017 American Physical Society
Physicists have developed a quantum machine learning algorithm that can handle infinite dimensions—that is, it works with continuous variables (which have an infinite number of possible values on a closed interval) instead of the typically used discrete variables (which have only a finite number of values).
The researchers, Hoi-Kwan Lau et al., have published a paper on generalizing quantum machine learning to infinite dimensions in a recent issue of Physical Review Letters.
As the physicists explain, quantum machine learning is a new subfield within the field of quantum information that combines the speed of quantum computing with the ability to learn and adapt, as offered by machine learning.
One of the biggest advantages of having a quantum machine learning algorithm for continuous variables is that it can theoretically operate much faster than classical algorithms. Since many science and engineering models involve continuous variables, applying quantum machine learning to these problems could potentially have far-reaching applications.
"Our work demonstrates the ability to take advantage of photonics to perform machine learning tasks on a quantum computer that could far exceed the speed of any conventional computer," coauthor George Siopsis at the University of Tennessee told Phys.org. "Quantum machine learning also offers potential advantages such as lower energy requirements owing to the ability to store more information per qubit, and a very low cost per qubit compared to other technologies."
Most quantum machine learning algorithms developed so far work only with problems involving discrete variables. Applying quantum machine learning to continuous-variable problems requires a very different approach.
To do this, the physicists had to develop a new set of tools that work with continuous variables. This involves replacing the logic gates that are used for discrete-variable states with physical gates, which work for continuous-variable states. Building up from these basic building blocks of the algorithm, the scientists then developed new methods that power the quantum machine learning problems, called subroutines, which are represented by matrices and vectors.
Although the results of the study are purely theoretical, the physicists expect that the new algorithm for continuous variables could be experimentally implemented using currently available technology. The implementation could be done in several ways, such as by using optical systems, spin systems, or trapped atoms. Regardless of the type of system, the implementation would be challenging. For example, an optical implementation that the scientists outlined here would require some of the latest technologies, such as "cat states" (a superposition of the "0" and "1" states) and high rates of squeezing (to reduce quantum noise).
In the future, the scientists hope to further investigate how continuous-variable quantum machine learning can be extended to replicate some of the latest results involving discrete variables. Another interesting avenue to pursue is a hybrid approach, which would combine the methods of both discrete and continuous variables in a single algorithm.
More information:
Hoi-Kwan Lau, Raphael Pooser, George Siopsis, and Christian Weedbrook. "Quantum Machine Learning over Infinite Dimensions." Physical Review Letters. DOI: 10.1103/PhysRevLett.118.080501
Also at arXiv:1603.06222 [quant-ph]
Journal information: Physical Review Letters
© 2017 Phys.org