Success by deception

Theoretical physicists from ETH Zurich deliberately misled intelligent machines, and thus refined the process of machine learning. They created a new method that allows computers to categorize data—even when humans have no idea what this categorization might look like.

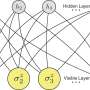
When computers independently identify bodies of water and their outlines in satellite images, or beat the world's best professional players at the board game Go, then adaptive algorithms are working in the background. Programmers supply these algorithms with known examples in a training phase: images of bodies of water and land, or sequences of Go moves that have led to success or failure in tournaments. Similarly to how our brain nerve cells produce new networks during learning processes, the special algorithms adapt in the learning phase based on the examples presented to them. This continues until they are able to differentiate bodies of water from land in unknown photos, or successful sequences of moves from unsuccessful ones.

Until now, these artificial neural networks have been used in machine learning with a known decision-making criterion: we know what a body of water is and which sequences of moves were successful in Go tournaments.

Separating wheat from chaff

Now, a group of scientists working under Sebastian Huber, Professor of Condensed Matter Theory and Quantum Optics at ETH Zurich, have expanded the applications for these neural networks by developing a method that not only allows categorisation of any data, but also recognises whether complex datasets contain categories at all.

Questions of this kind arise in science: for example, the method could be useful for analysis of measurements from particle accelerators or astronomical observations. Physicists could thus filter out the most promising measurements from their often unmanageable quantities of measurement data. Pharmacologists could extract molecules with a certain probability of having a specific pharmaceutical effect or side-effect from large molecular databases. And data scientists could sort huge masses of disordered data ripples and obtain usable information (data mining).

Search for a boundary

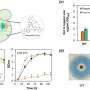
The ETH researchers applied their method to an intensively researched phenomenon of theoretical physics: a many-body system of interacting magnetic dipoles that never reaches a state of equilibrium - even in the long term. Such systems have been described recently, but it is not yet known in detail which quantum physical properties prevent a many-body system from entering a state of equilibrium. In particular, it is unclear where exactly the boundary lies between systems that reach equilibrium and those that do not.

In order to locate this boundary, the scientists developed the "act as if" principle: taking data from quantum systems, they established an arbitrary boundary based on one parameter and used it to divide the data into two groups. They then trained an artificial neural network by pretending to it that one group reached a state of equilibrium while the other did not. Thus, the researchers acted as if they knew where the boundary was.

Scientists confused the system

They trained the network countless times overall, with a different boundary each time, and tested the network's ability to sort data after each session. The result was that, in many cases, the network struggled to classify the data as the scientists had. But in some cases, the division into the two groups was very accurate.

The researchers were able to show that this sorting performance depends on the location of the boundary. Evert van Nieuwenburg, a doctoral student in Huber's group, explains this as follows: "By choosing to train with a boundary far away from the actual boundary (which I don't know), I am able to mislead the network. Ultimately we're training the network incorrectly - and incorrectly trained networks are very bad at classifying data." However, if by chance a boundary is chosen close to the actual boundary, a highly efficient algorithm is produced. By determining the algorithm's performance, the researchers were able to track down the boundary between quantum systems that reach equilibrium and those that do not: the boundary is located where the network's sorting performance is highest.

The researchers also demonstrated the capabilities of their new method using two further questions from theoretical physics: topological phase transitions in one-dimensional solids and the Ising model, which describes magnetism inside solids.

Categorisation without prior knowledge

The new method can also be illustrated in simplified form with a thought experiment, where we want to classify red, reddish, bluish and blue balls into two groups. We assume that we have no idea of how such a classification might reasonably look.

If a neural network is trained by telling it that the dividing line lies somewhere in the red region, then this will confuse the network. "You try to teach the network that blue and reddish balls are the same and ask it to differentiate between red and red balls, which it simply isn't able to do," says Huber.

On the other hand, if you place the boundary in the violet colour spectrum, the network learns an actual difference and sorts the balls into red and blue groups. However, one does not need to know in advance that the dividing line should be in the violet region. By comparing the sorting performance at a variety of chosen boundaries, this boundary can be found with no prior knowledge.