Scientists create a quantum computer memory cell of a higher dimension than a qubit

Scientists from the Institute of Physics and Technology of the Russian Academy of Sciences and MIPT have let two electrons loose in a system of quantum dots to create a quantum computer memory cell of a higher dimension than a qubit (a quantum bit). In their study published in Scientific Reports, the researchers demonstrate for the first time how quantum walks of several electrons can help to implement quantum computation.
"By studying the system with two electrons, we solved the problems faced in the general case of two identical interacting particles. This paves the way toward compact high-level quantum structures," says Leonid Fedichkin, associate professor at MIPT's Department of Theoretical Physics.
In a matter of hours, a quantum computer would be able to hack through the most popular cryptosystem used by web browsers. As far as more benevolent applications are concerned, a quantum computer would be capable of molecular modeling that accounts for all interactions between the particles involved. This in turn would enable the development of highly efficient solar cells and new drugs. To have practical applications, a quantum computer needs to incorporate hundreds or even thousands of qubits. And that is where it gets tricky.
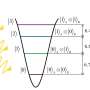
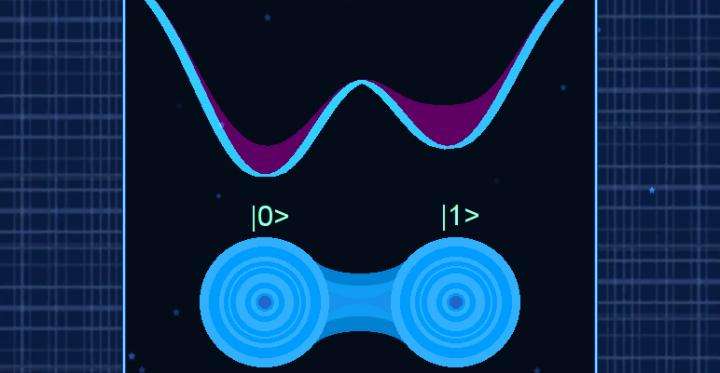
As it turns out, the unstable nature of the connection between qubits remains the major obstacle preventing the use of quantum walks of particles for quantum computation. Unlike their classical analogs, quantum structures are extremely sensitive to external noise. To prevent a system of several qubits from losing the information stored in it, liquid nitrogen (or helium) needs to be used for cooling. Plenty of schemes have been proposed for the experimental realization of a separate qubit. In an earlier study, a research team led by Prof. Fedichkin demonstrated that a qubit could be physically implemented as a particle "taking a quantum walk" between two extremely small semiconductors known as quantum dots, which are connected by a "quantum tunnel." From the perspective of an electron, the quantum dots represent potential wells. Thus, the position of the electron can be used to encode the two basis states of the qubit—|0? and |1?—depending on whether the particle is in one well or the other. Rather than sit in one of the two wells, the electron is smeared out between the two different states, taking up a definite position only when its coordinates are measured. In other words, it is in a superposition of two states.
If an entangled state is created between several qubits, their individual states can no longer be described separately from one another, and any valid description must refer to the state of the whole system. This means that a system of three qubits has a total of eight basis states and is in a superposition of them: A|000⟩+B|001⟩+C|010⟩+D|100⟩+E|011⟩+F|101⟩+G|110⟩+H|111⟩. By influencing the system, one inevitably affects all of the eight coefficients, whereas influencing a system of regular bits only affects their individual states. By implication, n bits can store n variables, while n qubits can store 2n variables. Qudits offer an even greater advantage, since n four-level qudits (aka ququarts) can encode 4n, or 2n×2n variables. To put this into perspective, 10 ququarts store approximately 100,000 times more information than 10 bits. With greater values of n, the zeros in this number start to pile up very quickly.
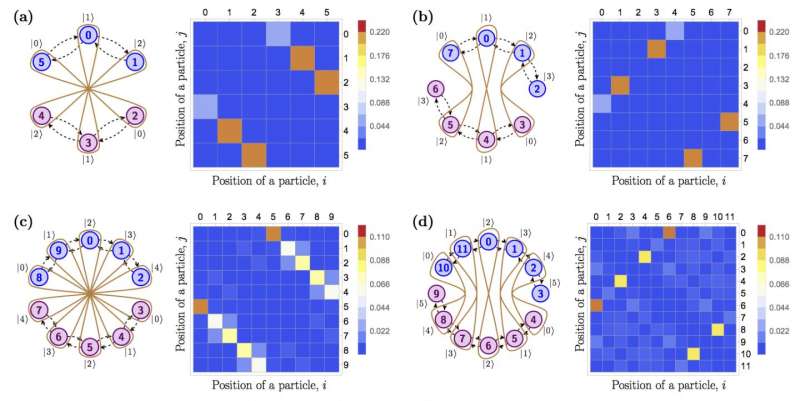
In this study, Alexey Melnikov and Leonid Fedichkin obtain a system of two qudits implemented as two entangled electrons quantum-walking around the so-called cycle graph. To make one, the scientists had to "connect the dots," forming a circle (once again, these are quantum dots, and they are connected by quantum tunneling). The entanglement of the two electrons is caused by the mutual electrostatic repulsion experienced by like charges. It is possible to create a system of even more qudits in the same volume of semiconductor material. To do this, it is necessary to connect quantum dots in a pattern of winding paths and have more wandering electrons. The quantum walks approach to quantum computation is convenient because it is based on a natural process. Nevertheless, the presence of two identical electrons in the same structure was a source of additional difficulties that had remained unsolved.
The phenomenon of particle entanglement plays a pivotal role in quantum information processing. However, in experiments with identical particles, false entanglement can arise between electrons that are not interacting, which must be distinguished from genuine entanglement. To do this, the scientists performed mathematical calculations for both cases, viz., with and without entanglement. They observed the changing distribution of probabilities for the cases with six, eight, 10, and 12 dots, i.e., for a system of two qudits with three, four, five, and six levels each. The scientists demonstrated that their proposed system is characterized by a relatively high degree of stability.
So far, scientists have been unable to connect a sufficient number of qubits for the development of a quantum computer. The work of the Russian researchers brings computer science one step closer to a future when quantum computations are commonplace. And although there are algorithms that quantum computers could never accelerate, others would still benefit enormously from devices able to exploit the potential of large numbers of qubits (or qudits). These alone would be enough to save us a couple of thousand years.
More information: Alexey A. Melnikov et al, Quantum walks of interacting fermions on a cycle graph, Scientific Reports (2016). DOI: 10.1038/srep34226
Journal information: Scientific Reports
Provided by Moscow Institute of Physics and Technology