July 8, 2016 report
Mathematical framework offers a more detailed understanding of network relationships
(Phys.org)—A trio of math and computer scientists has developed a means for developing generalized frameworks that allow for clustering networks based on higher-order connectivity patterns. In their paper published in the journal Science, Austin Benson and Jure Leskovec with Stanford University and David Gleich with Purdue University outline their framework ideas and offer real life examples of ways their techniques can be applied to help understand complex networks in simpler ways. Nataša Pržulj and Noël Malod-Dognin with University College London offer an analysis of the work done by the trio in a Perspectives piece in the same journal issue.
As the authors note, it is not difficult to make out patterns in very small networks, a person trying to do so need only watch the system at work for a period of time. It is when networks become bigger and more complex that they become unwieldy. Even in such cases, however, low-order patterns are often still easy to discern—counting nodes or edges for example, offers some degree of network size, though doing so tells you very little about what the network does and how—that is where high-order organizational principles come into play. Unfortunately attempts to create a means for providing more information or detail about such systems has to date, not met with much success. In this new effort, the researchers describe a framework they have developed that offers some of the pattern recognition seen in smaller networks, with more complex networks.
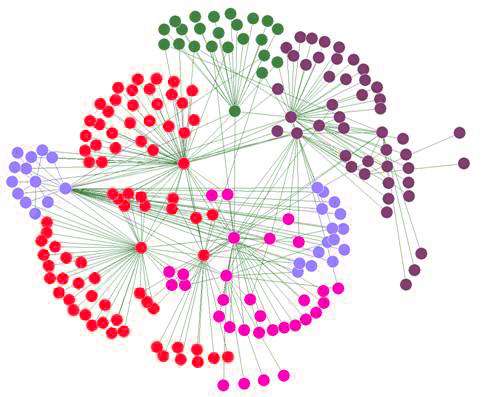
They start, Pržulj and Malod-Dognin note, with one of the more common higher-order structures known as small network subgraphs, which they refer to as network motifs—those that are statistically significant can be used as building blocks for the building of a mathematical framework, which is of course what the researchers have done. Relationship identification among the motifs was done by applying clustering algorithms. The result is a framework that highlights and/or identifies which of the motifs are the most critical when a network is in operation.
The trio tested their framework technique by using it to analyze part of the neuronal network of a roundworm, and report that it revealed the particular cluster of 20 neurons responsible for performing actions such as standing and wiggling its head. They also gained insights into air traffic patterns by using it to perform an analysis of airports in the U.S. and Canada. They suggest such frameworks may be used in a wide variety of applications.
More information: A. R. Benson et al. Higher-order organization of complex networks, Science (2016). DOI: 10.1126/science.aad9029
Abstract
Networks are a fundamental tool for understanding and modeling complex systems in physics, biology, neuroscience, engineering, and social science. Many networks are known to exhibit rich, lower-order connectivity patterns that can be captured at the level of individual nodes and edges. However, higher-order organization of complex networks—at the level of small network subgraphs—remains largely unknown. Here, we develop a generalized framework for clustering networks on the basis of higher-order connectivity patterns. This framework provides mathematical guarantees on the optimality of obtained clusters and scales to networks with billions of edges. The framework reveals higher-order organization in a number of networks, including information propagation units in neuronal networks and hub structure in transportation networks. Results show that networks exhibit rich higher-order organizational structures that are exposed by clustering based on higher-order connectivity patterns.
Journal information: Science
© 2016 Phys.org