Discrete convex analysis for analysis of iterative auctions
Researchers are investigating auction models where there are many different indivisible goods such as houses and cars. Notably, algorithms known as iterative auctions are often used to compute equilibrium prices of goods.
However, the theoretical behavior of iterative auction algorithms is not fully understood. In particular, there are only a few scattered results of research on the theoretical analysis for time bounds of iterative auctions to-date, even though the theoretical bounds on the number of iterations are interesting as research topics in their own right and important for practical applications.
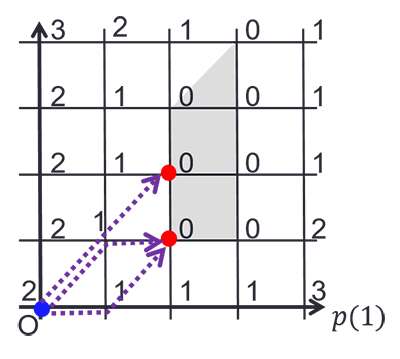
Here, Akiyoshi Shioura at Tokyo Tech and colleagues at Tokyo Metropolitan University, and University of York, UK, describe a unified method of analysis for iterative auctions based on discrete convex analysis—a theory of discrete optimization problems. A key tool in the analysis is the concept of the Lyapunov function in auction theory. The researchers show that the Lyapunov function has a useful property called discrete convexity. By making use of this property, the team derived exact bounds on the number of iterations in terms of the distance between the initial price vector and the resulting equilibrium.
The results of this research extend and unify the iterative auction algorithms for a variety of auction models, offering computational complexity results for these algorithms, and reinforcing the connection between auction theory and discrete convex analysis.
More information: Kazuo Murota et al. Time bounds for iterative auctions: A unified approach by discrete convex analysis, Discrete Optimization (2016). DOI: 10.1016/j.disopt.2016.01.001
Provided by Tokyo Institute of Technology