March 11, 2016 report
Physics pair show that Ising model can be used as a universal spin model

(Phys.org)—A pair of physicists has shown that it is possible to transform disparate spin models into different types of just one simple model. In their paper published in the journal Science, Gemma De las Cuevas, with the Max Planck Institute for Quantum Optics and Toby Cubitt, with University College London, offer a proof to show that any spin model can be converted to the relatively simple Ising model. Stephanie Wehner with QuTech, Delft University of Technology offers a Perspectives piece on the work done by the team in the same journal issue, outlining the proof and explaining how and why a universal spin model would be useful.
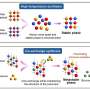
Spin models were first developed as a means to help explain the properties of magnetic materials—the magnetism in each atom originates from the spin of an unpaired electron within it. The first was created by Wilhelm Lenz, who handed it off to Ernest Ising, who used it to show that spins should undergo phase transitions below a certain temperature. Since that time, spin models have been developed for a wide variety of applications, perhaps most notably in particle physics. Now, in this new effort, De las Cuevas and Cutitt show that it is possible to transform any of these other newer models into the 2D Ising model, including 3D models.
Their proof has two main parts, the first involved showing that any Ising model is equivalent to an instance of a satisfiability problem and showing a way to match such problems to an Ising model. The second part involved showing how any spin model could be converted to a satisfiability problem and then translated to an Ising model.

The benefit of having a universal model, Wehner explains, is that it offers an alternative way for scientists to run their models, particularly on a computer. If a 3D model is extremely complex, for example, or requires an untenable number of cycles to run, there is a chance it could be configured to run as an Ising model. But she notes that it could also be used as a means for melding the work being done by physicists and computer scientists, helping to further explain the workings of nature.
More information: G. De las Cuevas et al. Simple universal models capture all classical spin physics, Science (2016). DOI: 10.1126/science.aab3326
Abstract
Spin models are used in many studies of complex systems because they exhibit rich macroscopic behavior despite their microscopic simplicity. Here, we prove that all the physics of every classical spin model is reproduced in the low-energy sector of certain "universal models," with at most polynomial overhead. This holds for classical models with discrete or continuous degrees of freedom. We prove necessary and sufficient conditions for a spin model to be universal and show that one of the simplest and most widely studied spin models, the two-dimensional Ising model with fields, is universal. Our results may facilitate physical simulations of Hamiltonians with complex interactions.
Journal information: Science
© 2016 Phys.org